Wiskundigen zijn al tientallen jaren gefascineerd door aperiodieke betegeling: het in elkaar passen van vormen om oneindige patronen te maken die zich nooit herhalen. Nu blijkt dat je zo’n niet-herhalend tegelpatroon met één enkele vorm kunt maken.
Wiskundigen hebben een enkele vorm ontdekt waarmee een oppervlak van willekeurige grootte volledig kan worden bedekt, zonder dat er ooit een repeterend patroon ontstaat. Het heeft tientallen jaren geduurd om deze verrassend eenvoudige vorm te vinden. De vorm kan op allerlei vlakken van pas komen – van materiaalwetenschap tot decoratiewerk.
Roger Penrose
Er bestaan allerlei simpele vormen, zoals vierkanten en gelijkzijdige driehoeken, die een oppervlak volledig kunnen bedekken. Dat doen ze in een herhalend patroon dat iedereen die weleens naar een badkamermuur heeft gestaard bekend zal voorkomen.
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
Wiskundigen zijn geïnteresseerd in een complexere versie van tegelwerk, bekend als aperiodieke betegeling. Daarbij worden vormen gebruikt die samen nooit een repeterend patroon vormen.
De beroemdste aperiodieke tegels zijn gemaakt door wiskundige Roger Penrose. Hij ontdekte in de jaren ’70 twee vormen die gecombineerd kunnen worden tot een oneindig, nooit herhalend tegelpatroon.
Computers en vernuft
Nu hebben wiskundige Chaim Goodman-Strauss van de Universiteit van Arkansas en zijn collega’s een enkele tegelvorm gevonden die datzelfde doet. Ze noemden de vorm ‘de hoed’.
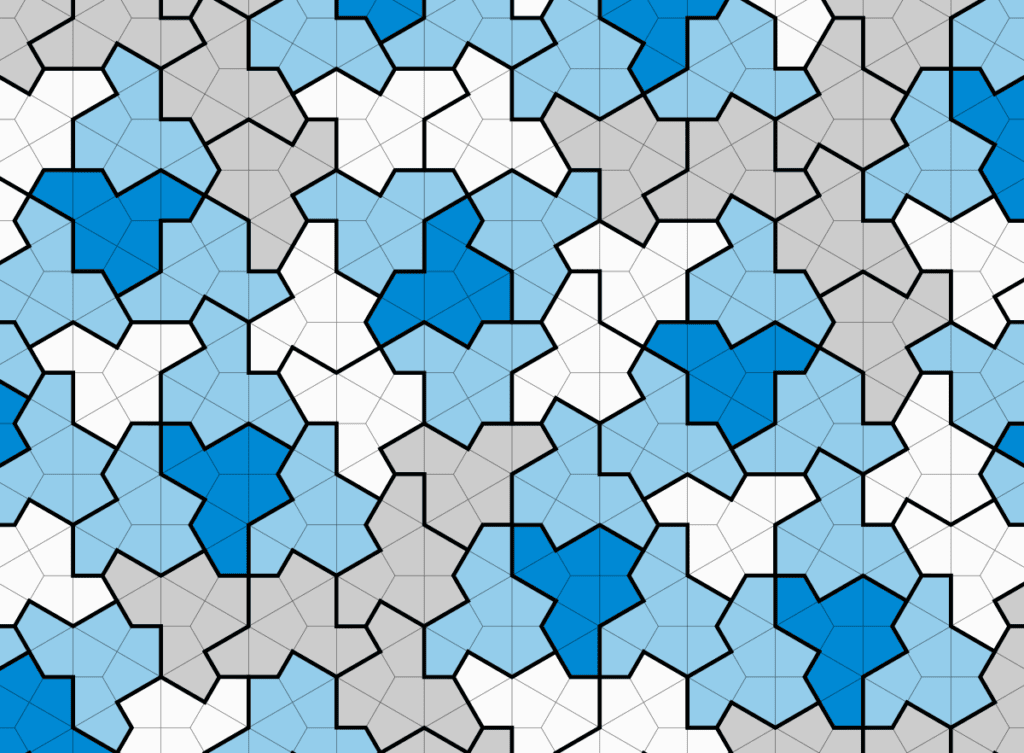
Volgens Goodman-Strauss vereiste hun ontdekking krachtige computers en menselijk vernuft, zowel voor het vinden van de tegel als voor het bewijzen dat hij aperiodiek is. Eerst gebruikten de wiskundigen computers om een heleboel mogelijke tegels te elimineren. Vervolgens benutten ze hun eigen expertise om een correcte vorm te vinden en het bewijs rond te krijgen.
Het team vond twee bewijzen voor de hoed. Een daarvan is gebaseerd op een openbaar gemaakte computercode.
‘Je zoekt letterlijk naar iets van één op een miljoen. Je filtert de 999.999 saaie eruit, dan heb je iets geks, en dat is het dan waard om verder te onderzoeken’, zegt Goodman-Strauss. ‘Dat ga je dan met de hand onderzoeken en proberen te begrijpen, daar ga je de structuur uit halen. Op dat gebied zou een computer nutteloos zijn, aangezien een mens betrokken moet zijn bij het opstellen van een bewijs dat een mens kan begrijpen.’
Einstein
Zo’n enkele vorm staat bekend als een ‘einstein’ (van het Duitse ‘ein stein’, oftewel ‘één steen’). Tot nu toe was het niet eens duidelijk of er wel een einstein bestaat. Wiskundige Sarah Hart van de Universiteit van Londen, niet bij het onderzoek betrokken, achtte het onmogelijk. ‘Er zijn oneindig veel mogelijke kandidaat-stenen. Dat er überhaupt een oplossing bestaat, voelt nogal contra-intuïtief’, zegt ze.
Hoewel de hoed decennialang door wiskundigen over het hoofd is gezien, is het geen ingewikkelde vorm. De einstein heeft slechts 13 zijden. De vorm behoudt bovendien zijn aperiodieke eigenschappen wanneer je de lengte van de zijden varieert. Dat betekent dat de gevonden oplossing eigenlijk een continuüm van soortgelijke vormen is.
Badkamer
Volgens Hart kan kennis van aperiodieke tegelvormen ons helpen materialen te ontwerpen die buitengewoon sterk zijn of andere nuttige eigenschappen hebben. In kristalstructuren kunnen wel-herhalende patronen namelijk leiden tot kwetsbare lijnen, waarlangs het materiaal kan breken.
‘Alleen bepaalde vreemde en wonderlijke soorten kristalstructuren, quasikristallen genaamd, vertonen aperiodiciteit’, zegt ze. ‘Dit nieuwe tegelpatroon kan ons begrip van de mogelijke structuren in quasikristallen vergroten.’
Wiskundige Colin Adams van het Williams College in Massachusetts was verbijsterd door de eenvoud van de oplossing. Volgens hem liet dit probleem zich niet gemakkelijk oplossen met berekeningen die uitgaan van brute kracht. Hij zou het tegelpatroon graag in de praktijk terugzien.
‘Je zult zien dat mensen dit patroon in hun badkamer gaan aanbrengen, gewoon omdat het cool is. Als ik mijn badkamer nu zou gaan betegelen, zou ik het ook aanbrengen’, zegt hij.
