Waarnemingen van botsende zwarte gaten zijn inmiddels doodnormaal. Maar hoe deze duistere koppels ontstaan, is nog een open vraag. Een statistische oplossing van Newtons drielichamenprobleem steunt het idee dat ze een duwtje hebben gekregen van een derde zwart gat.
De afgelopen jaren hebben metingen van zwaartekrachtsgolven tientallen koppels van botsende zwarte gaten aan het licht gebracht. Van die koppels wordt aangenomen dat ze ontstaan uit systemen van twee zware sterren. De sterren in zo’n dubbelstersysteem zouden dan allebei afzonderlijk instorten tot een zwart gat, waarna ze steeds dichter om elkaar heen draaien en uiteindelijk samensmelten.
Deze theorie heeft echter één groot probleem. Volgens de meeste computermodellen smelten twee zware sterren die dicht bij elkaar ontstaan al samen voordat ze in twee zwarte gaten kunnen veranderen. En wanneer ze ver van elkaar ontstaan, komen ze ook na de transformatie in zwarte gaten niet bij elkaar – of tenminste niet binnen 14 miljard jaar, de huidige leeftijd van het heelal.
‘Als we iets buitenaards ontmoeten, dan is het een machine’
Oude sterren en pril leven – dat zijn de onderwerpen waar het hart van sterrenkundige Leen Decin harder van gaat kloppen.
Een andere mogelijke verklaring voor de waargenomen botsingen is dat een derde zwart gat de twee zwarte gaten die uit een dubbelster ontstaan naar elkaar toe duwt. Deze verklaring is echter heel moeilijk te testen. Wanneer drie zwarte gaten elkaar ontmoeten, kan er van alles gebeuren. Het kost veel te veel computertijd om al die afzonderlijke scenario’s te simuleren.
Wellicht kunnen astronomen dit obstakel binnenkort omzeilen. Astrofysici Nicholas Stone en Nathan Leigh ontwikkelden namelijk een statistische oplossing voor het beroemde drielichamenprobleem van Newton. Daarmee kunnen astronomen de uitkomst van een ontmoeting van drie zwarte gaten beter voorspellen. Het resultaat is eind december gepubliceerd in Nature.
Kosmische stoelendans
Het drielichamenprobleem gaat over de beweging van drie hemellichamen die zwaartekracht van elkaar ondervinden. Met de zwaartekrachtswetten van Newton is van twee hemellichamen eenvoudig uit te rekenen hoe ze om elkaar heen zullen draaien. Wanneer er een derde object in het spel is, worden de berekeningen echter uitermate complex. Met name wanneer de drie objecten een vergelijkbare massa hebben, wordt hun beweging al gauw compleet onvoorspelbaar.
Om een beetje orde in die chaos te brengen, simuleerden de twee astrofysici de beweging van enkele honderdduizenden systemen van drie objecten. Daarbij gingen ze telkens uit van een systeem van twee objecten waar een derde object in de buurt komt. Er ontstaat dan een soort kosmische stoelendans, die op zichzelf onvoorspelbaar is, maar wél telkens dezelfde uitkomst heeft.
Scramble
Neem bijvoorbeeld een koppel van zwarte gaten dat bezoek krijgt van een derde zwart gat. Het derde zwarte gat cirkelt dan lange tijd op een afstandje rond de andere twee. Maar op een gegeven moment komen de drie objecten dicht bij elkaar, wat leidt tot een korte periode van enorme chaos – de astrofysici noemen dat een scramble.
Zo’n scramble eindigt wanneer een van de drie zwarte gaten genoeg energie heeft om het strijdgewoel te verlaten. Dat kan het ingevangen zwarte gat zijn, maar ook eentje van het oorspronkelijke tweetal. Dat energieke zwarte gat is dan aan de beurt om van een afstandje rond de andere twee te cirkelen. Deze relatief stabiele toestand houdt weer een tijdlang aan, tot de drie zwarte gaten opnieuw bij elkaar komen en de volgende kortstondige scramble begint.
Vroeg of laat houdt deze stoelendans echter op. Dat gebeurt wanneer een van de zwarte gaten in een scramble zoveel energie krijgt, dat die volledig bij de andere twee wegvliegt. Wat overblijft is een nieuw koppel van zwarte gaten, dat lange tijd stabiel blijft.
Bijna-botsingen
Het was al bekend dat een instabiel systeem van drie ongeveer even zware objecten uiteindelijk uitmondt in een relatief stabiel tweetal. Maar het resulterende koppel kan nog steeds allerlei eigenschappen hebben. ‘Voor die chaotische bijna-botsingen tussen drie objecten is geen simpele formule beschikbaar. Je moet met een computer stapje voor stapje de banen uitrekenen’, zegt astronoom Selma de Mink, universitair hoofddocent aan de Universiteit van Amsterdam en de Harvard Universiteit. ‘Dat is op zich niet moeilijk, maar je wilt dit eigenlijk heel vaak uitrekenen voor telkens net iets andere massa’s en richtingen.’
Met de nieuwe statistische oplossing kunnen astronomen dat probleem omzeilen door de waarschijnlijkheid van verschillende uitkomsten te berekenen. Zo kunnen ze bijvoorbeeld de kans uitrekenen dat een derde zwart gat twee andere zwarte gaten dichter bij elkaar brengt – dicht genoeg om langzaam naar elkaar toe te bewegen en binnen afzienbare tijd samen te smelten.
Onlangs is er voor het eerst een sterrenstelsel gevonden dat drie zwarte gaten bevat. Ook ontdekten astronomen vorig jaar drie zwarte gaten die op ramkoers lijken te liggen. Deze vondsten wijzen erop dat systemen van drie zwarte gaten misschien wel vaker voorkomen dan voorheen gedacht.
Mantel van waterstof
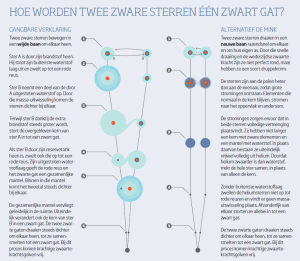
Er zijn echter ook andere verklaringen voor het botsen van zwarte gaten. De meest gangbare is dat twee zware sterren in een wijd dubbelstersysteem massa uitwisselen. Wanneer een van de sterren in een zwart gat is veranderd, krijgen de twee een gezamenlijke ‘mantel’ van waterstof. Die mantel geeft ze de gelegenheid om dichter bij elkaar te komen, waarna ook de tweede ster in een zwart gat verandert.
Daarnaast zijn er enkele alternatieve scenario’s. Zo bedacht De Mink een model dat uitgaat van twee ‘misvormde’ sterren in een nauw dubbelstersysteem. De sterren draaien zo snel om elkaar en hun eigen as, dat ze een soort druppelvorm krijgen. Daardoor vermengen ze volledig met elkaar, wat verhindert dat ze samensmelten voordat ze in een zwart gat veranderen.
Het is onmogelijk om zeker te weten welk scenario ten grondslag ligt aan een waargenomen botsing tussen twee zwarte gaten. Astronomen kunnen dat proces, dat honderdduizenden of zelfs miljoenen jaren duurt, niet van begin tot eind volgen. Het enige wat ze kunnen doen, is simulaties verbeteren.
De Mink hoopt dan ook dat het resultaat simulaties van de beweging van drie objecten sneller en nauwkeuriger zal maken. ‘Triples zijn erg interessant en hip. Er zijn veel sterren in triples, maar we weten er nog maar weinig van. Ik denk dat triples heel veel potentie hebben’, zegt ze. ‘In eerste instantie is dit belangrijk voor de dans van drie zwarte gaten. Zwarte gaten leven lang en hebben veel tijd voor dit soort interacties.’
