Deeltjesfysicus Tristan du Pree waagt graag een gokje, maar niet in de wetenschap.
Tijdens de zomer – het lijkt alweer een eeuwigheid geleden – zijn we er een weekje met de tent op uitgetrokken. Vanaf het Cern bij Genève, via allerlei Alpencols, is er een prachtige route naar de kust van de Middellandse Zee. En aangezien we toen toch in de buurt waren, zijn we gelijk ook maar even langs Monaco gegaan. Je komt immers niet elke dag in een dwergstaat.
Een van de publiekstrekkers van het vorstendom is het casino van Monte Carlo. Dat gokpaleis is zo bekend dat zelfs de simulatie van random getallen in ons wetenschappelijk onderzoek hiernaar is vernoemd. En dus begin je in de zonnige haven, naast het Formule 1-parcours, toch weer te rekenen: hoe groot is de kans dat we nu, met vier dobbelstenen vier keer hetzelfde zou werpen?
Kosmische curiosa: quasimaan Kamo’oalewa
Sterrenkundejournalist Govert Schilling beschrijft elke maand een wonderlijke bewoner van het heelal. In deze editie: quasimaan Kamo’oalewa.
Nou ja, de kans dat je met één worp vier keer zes gooit, met vier dobbelstenen, is eenvoudig uit te rekenen: de vermenigvuldiging (1/6)x(1/6)x(1/6)x(1/6) levert een kans van minder dan één op duizend. Dat is dus redelijk onwaarschijnlijk.
Onbetrouwbare intuïtie
Maar de kans dat ik, ofwel mijn tafelgenoot, tijdens een beurt vier gelijke getallen werpt zonder dat het uitmaakt welk getal (vier enen, vier tweeën, …) is na het optellen van alle mogelijke worpen dan nog maar ongeveer één op honderd. Alweer een stuk minder onwaarschijnlijk dus. En daar lijkt een dobbelspelletje al weer veel op onderzoek bij de LHC.
Als wij achteraf onze data bekijken (oftewel de geworpen dobbelstenen op tafel) en denken iets uitzonderlijks te zien, dan ligt de waarschijnlijkheid namelijk ook aan de hypotheses die je test (welke worp je vooraf had gehoopt te zien) en het aantal metingen dat je verricht (het aantal tafelgenoten en beurten). Het kwantificeren van de toevalligheid van een bepaalde worp is daardoor een delicate kwestie, waarbij je niet altijd op intuïtie kan vertrouwen.
En die intuïtie zorgde er anderhalf jaar geleden ook voor, bij de bekendmaking van nieuwe LHC-resultaten, dat er heel wat theoreten artikelen publiceerden over resultaten van het Atlas-experiment en het CMS-experiment met een kans van ongeveer één op duizend. Het onderbuikgevoel was onterecht, en het signaal bleek later niet genoeg voor een ontdekking.
|
|
 |
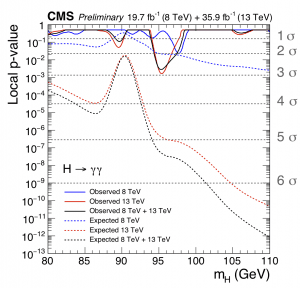Dat is dan ook de reden dat we de statistische lat voor een ontdekking in de experimentele natuurwetenschappen heel hoog leggen. Voordat de experimentatoren een ontdekking claimen, zoals bij het higgsboson, eisen wij namelijk vijf sigma, ofwel onwaarschijnlijker dan één op miljoen.
Spannend hobbeltje
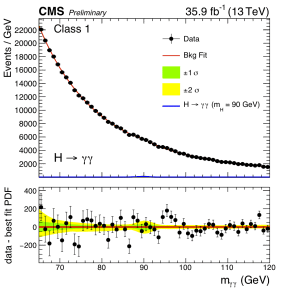
Het nieuwe resultaat van CMS, hierboven, haalt deze significantie niet. De kans op een dergelijk signaal, bij een massa rond de 95 GeV, is momenteel rond de drie sigma, oftewel ongeveer één op duizend. En na het in ogenschouw nemen van het effect dat we ook elders naar nieuwe signalen zoeken, is de onwaarschijnlijkheid nog geen twee sigma, oftewel minder dan één op honderd.
En toch, ondanks de macht van de getallen, blijft het spannend om een dergelijk hobbeltje in de data te zien. Wellicht, heel misschien, is het dit keer geen toeval! Als de wiedeweerga weer terug van Monte Carlo naar Genève dus.