Wiskundigen hebben vormen ontdekt die in elke dimensie een constante breedte hebben. Deze vormen zijn niet rond, maar toch kunnen ze rollen als een wiel.
Wiskundigen hebben opnieuw het wiel uitgevonden. Ze hebben vormen ontdekt die soepeltjes rollen wanneer ze tussen twee oppervlakken zitten ingeklemd. Dat doen ze niet alleen in de twee of drie ruimtelijke dimensies die we allemaal kennen, maar zelfs in vier, vijf of meer dimensies.
De objecten waar het om gaat, staan bekend als vormen met een constante breedte. De meest bekende in twee en drie dimensies zijn de cirkel en de bol. Maar er zijn meer vormen die aan deze beschrijving voldoen. Een voorbeeld is de driehoek van Reuleaux: een driehoek met gekromde randen.

‘AI is een veredelde rekenmachine’
Met AI spoort Ann Dooms vervalste schilderijen op, maakt ze onleesbare teksten doorzoekbaar en brengt ze de kwaliteit van eicellen in kaart.
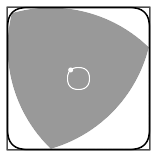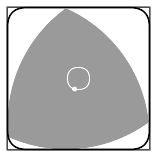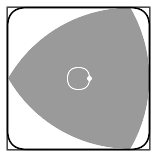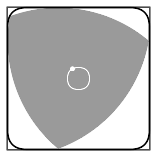
Beeld: Wikimedia Commons/LEMeZza, CC BY 3.0
Ook bestaat de regelmatige zevenhoek van Reuleaux. Deze vorm komt ‘in het echt’ voor bij sommige muntstukken. In het Verenigd Koninkrijk hebben bijvoorbeeld de 50 pence-munten deze vorm, en in Gambia de dalasi. De constante breedte van de muntjes zorgt ervoor dat ze gemakkelijk automaten inrollen en altijd worden herkend, ongeacht hun oriëntatie.

Beeld: WikiMedia Commons/Numizmat 675, CC BY-SA 3.0
Kleiner dan een bol
Belangrijk is dat al deze vormen een kleiner oppervlak of volume hebben dan een cirkel of bol met dezelfde breedte. Tot nu toe was niet bekend of hetzelfde ook in hogere dimensies geldt. Die vraag werd voor het eerst gesteld in 1988 door de Israëlisch-Amerikaanse wiskundige Oded Schramm. Hij vroeg zich dus af of er meerdimensionale objecten bestaan met een constante breedte die kleiner zijn dan het equivalent van een bol in hetzelfde aantal dimensies.
Het is helaas onmogelijk om een plaatje te maken van een vorm met meer dan drie dimensies. Wiskundigen bedenken ze door 2D- en 3D-vormen op logische manieren met extra dimensies uit te breiden.
Neem als voorbeeld een cirkel of een bol. Dat is een verzameling punten die zich op een constante afstand van een centraal punt bevinden. Diezelfde regel kun je opleggen in meer dimensies. ‘Soms ontdek je de meest fascinerende fenomenen als je naar steeds hogere dimensies kijkt’, zegt wiskundige Gil Kalai van de Hebreeuwse Universiteit van Jeruzalem in Israël.
Nu heeft wiskundige Andrii Arman van de Universiteit van Manitoba in Canada met zijn collega’s de vraag van Schramm beantwoord. De wiskundigen hebben een reeks vormen gevonden met een constante breedte in elke dimensie. Al die vormen zijn inderdaad kleiner dan een bol met een gelijkwaardig aantal dimensies.
Arman en zijn collega’s werkten al enkele jaren in wekelijkse vergaderingen aan dit probleem. ‘Je zou kunnen zeggen dat we aan dit probleem hebben gewerkt totdat het [eindelijk] meegaf’, zegt hij.
Opdelen in stukjes
De onderzoekers stelden zich een bol voor met ‘n’ dimensies, waarbij n elk getal mag zijn. Deze verdeelden ze vervolgens in 2n gelijke delen. Een (tweedimensionale) cirkel wordt dus in vier stukken verdeeld, een (driedimensionale) bol in acht stukken, een 4D-bol in 16 stukken, enzovoort. De onderzoekers rekten deze segmenten vervolgens uit en drukten ze ineen om hun vorm te veranderen zonder dat hun breedte veranderde. ‘Het recept is heel eenvoudig, maar dat begrepen we pas nadat we het hadden uitgewerkt’, zegt teamlid Andriy Bondarenko van de Noorse Universiteit voor Wetenschap en Technologie.
Het team bewees dat het altijd mogelijk is om een zodanige vervorming uit te voeren dat je een vorm krijgt met een volume dat maximaal 0,9n keer dat van de bol is in hetzelfde aantal dimensies. Dit betekent dat als je naar steeds hogere dimensies gaat, de vorm met constante breedte steeds kleiner wordt vergeleken met de bol.
Silhouet
Het is moeilijk om dit in een plaatje voor je te zien. Een trucje is om je het silhouet van de meerdimensionale vorm voor te stellen, dat dus één dimensie minder heeft. Zo lijkt de 3D-vorm vanuit de juiste hoek op een tweedimensionale driehoek van Reuleaux. Op dezelfde manier kan de 3D-vorm gezien worden als een ‘schaduw’ van de 4D-vorm, enzovoort. ‘De vormen in meer dimensies zullen in zekere zin vergelijkbaar zijn, maar nemen in complexiteit toe’, zegt Arman.
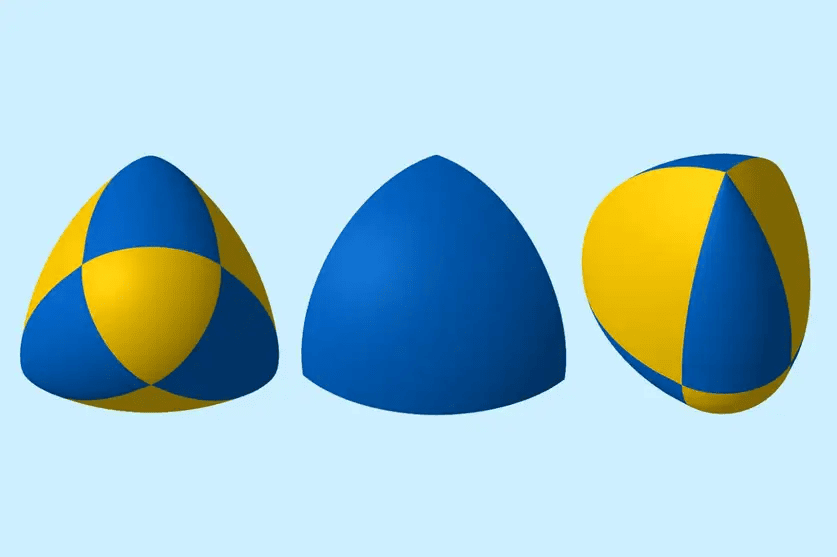
Beeld: Andriy Prymak et al. 2024/SageMath/Danylo Radchenko.
De wiskundigen willen deze nieuwe vormen verder bestuderen. ‘Zelfs met dit resultaat, dat een deel van het mysterie over [deze vormen] wegneemt, zijn het zeer mysterieuze verzamelingen in hoge dimensies’, aldus Kalai.

