Tot voor kort was het bijna onmogelijk om te berekenen hoe drie objecten in stabiele banen om elkaar heen kunnen draaien. Wiskundigen hebben nu een recordaantal nieuwe oplossingen gevonden.
Drie hemellichamen kunnen in stabiele banen om elkaar heen bewegen. Neem bijvoorbeeld de zon, de aarde en de maan. De vraag of er ook andere manieren zijn om drie stabiele banen te creëren, houdt wiskundigen al meer dan driehonderd jaar bezig. Nu hebben onderzoekers maar liefst 12.000 mogelijke configuraties gevonden.
Grote stappen
Het wiskundig beschrijven van de onderlinge zwaartekracht en de beweging van twee hemellichamen is relatief eenvoudig. Maar het probleem wordt direct veel complexer zodra er een derde object in het spel is.
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
In 2017 vonden onderzoekers 1223 nieuwe oplossingen voor het drielichamenprobleem. Dat was toen een verdubbeling van het bekende aantal mogelijkheden.
Nu doet computerwetenschapper Ivan Hristov van de Universiteit van Sofia in Bulgarije samen met zijn collega’s daar een schepje bovenop. Zij hebben 12.392 banen gevonden die volgens de wetten van Newton werken.
Vrije val
Het team gebruikte een supercomputer en een verbeterde versie van het algoritme uit 2017. Hristov zegt dat als hij de zoektocht zou herhalen met nog krachtigere hardware, hij er nog ‘vijf keer zoveel’ zou vinden.
Om de oplossingen te vinden, begonnen de onderzoekers met een simulatie van drie stilstaande objecten. Vervolgens lieten ze het drietal in vrije val omlaag tuimelen. Tijdens het vallen werden de objecten naar elkaar toe getrokken door de zwaartekracht. Hun impuls zorgt ervoor dat ze langs elkaar heen bewegen, afremmen, stoppen en dan weer naar elkaar toe trekken. Het team ontdekte dat als er geen wrijving bestaat, dit patroon zich oneindig herhaalt.
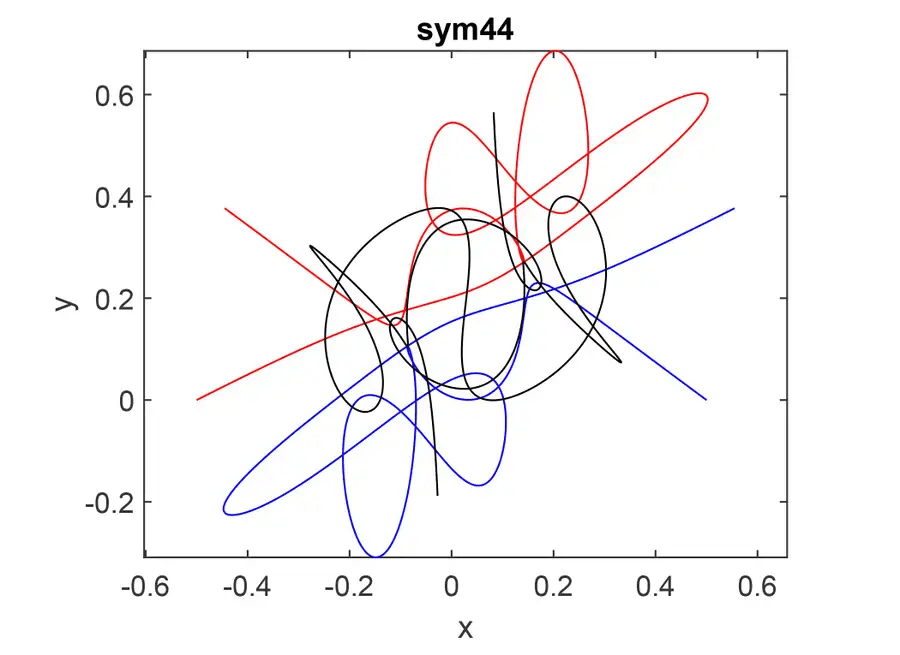
Oplossingen voor het drielichamenprobleem zijn interessant voor astronomen, omdat ze beschrijven hoe bijvoorbeeld sterren, planeten of manen een stabiele baan kunnen vinden. Maar het valt nog te bezien of de nieuwe oplossingen echt in het heelal voorkomen. Daar spelen minieme extra invloeden een rol, zoals de zwaartekracht van verdergelegen hemellichamen.
‘De relevantie voor de astronomie zal duidelijk worden nadat we de stabiliteit [van de banen] hebben bestudeerd – die is erg belangrijk’, zegt Hristov. ‘Desalniettemin – stabiel of instabiel – zijn ze van groot theoretisch belang. Ze hebben een hele mooie structuur in de ruimte en tijd.’
Echte wereld
Astronoom Juhan Frank van de staatsuniversiteit van Louisiana zegt dat het vinden van zoveel oplossingen onder deze precieze voorwaarden interessant is voor wiskundigen, maar dat het van beperkte toepassing is in de echte wereld. ‘De meeste, zo niet alle [oplossingen], vereisen zulke precieze beginvoorwaarden, dat ze waarschijnlijk nooit in de natuur worden voorkomen’, zegt Frank.
‘Na een complexe, maar voorspelbare baaninteractie hebben zulke drielichamensystemen de neiging om op te breken in een binair systeem en een ontsnappend derde lichaam’, stelt Frank. Dat wil zeggen dat twee van de hemellichamen bij elkaar blijven, en het derde object, meestal het object met de minste massa, wegvliegt.
