Het achtdamesprobleem is een wiskundig schaakprobleem dat in 1850 is opgelost. Nu is er ook een oplossing voor een uitgebreide versie van het probleem, waarbij je een heleboel dames op een enorm schaakbord plaatst.
Stel: je hebt een normaal schaakbord van acht bij acht vakjes. Kun je dan acht dames zodanig neerzetten dat ze elkaar geen van allen aanvallen? Dit ‘achtdamesprobleem’ stamt uit 1848. Twee jaar later waren alle 92 de oplossingen bekend (zie kader onderaan).
In 1869 publiceerde de Franse wiskundige Eugène Lionnet in Nouvelles Annales de Mathématiques een algemene versie van het probleem: op hoeveel manieren kun je op een schaakbord van n bij n vakjes n dames zodanig neerzetten dat ze elkaar niet aanvallen?
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
Bij dit n-damesprobleem loopt het aantal mogelijkheden heel snel op. Bij tien dames zijn er 352 manieren, bij vijftien dames zijn het er ruim 2 miljoen en bij twintig dames ruim 39 miljard. Het hoogste aantal dames waarbij het exacte aantal mogelijkheden is uitgerekend, is 27. Hierbij zijn er 234.907.967.154.122.528 mogelijkheden.
34 novemdeciljoen
In deze snelle stijging zit geen vast patroon. Je kunt dus geen formule opstellen om het aantal manieren voor een bepaald aantal dames precies uit te rekenen.
De Amerikaanse wiskundige Michael Simkin van de Harvard-universiteit heeft onlangs wel een formule opgesteld waarbij je het aantal mogelijkheden bij grote schaakborden – vanaf enkele tientallen dames – vrij dicht kunt benaderen. Hij ontdekte dat de dames dan op ongeveer (0,143n)n manieren kunnen worden neergezet.
Dat betekent dat er voor het honderddamesprobleem ongeveer 14,3¹⁰⁰ = 3,4 × 10115 oplossingen zijn, oftewel 34 novemdeciljoen – een getal van 116 cijfers. Bij het duizenddamesprobleem krijg je een onnoemelijk groot getal van 2154 cijfers. Bij het miljoendamesprobleem loopt het aantal cijfers zelfs op tot zo’n vijf miljoen.
Onder- en bovengrens
Simkin kwam op deze formule door te onderzoeken hoe de dames zich op zo’n megaschaakbord meestal zouden verdelen. Zouden ze bijvoorbeeld vooral in het midden van het bord komen te staan, of meer aan de randen? Door te focussen op de vakjes die de grootste kans maken te worden bezet, berekende de wiskundige een onder- en bovengrens voor het aantal mogelijke oplossingen.
De formule geeft de waarde die precies tussen deze grenzen inzit. De grenzen zitten relatief dicht bij elkaar, zodat de formule het aantal mogelijkheden goed benadert. Als je een bepaalde voorwaarde over de verdeling van de dames meegeeft, kan Simkin bij elk aantal dames zelfs het exacte aantal mogelijkheden uitrekenen.
Met zijn onderzoek heeft Simkin het n-damesprobleem nog niet schaakmat gezet. In theorie moet er een formule te vinden zijn die het aantal mogelijkheden nog dichter benadert. Dat laat Simkin echter graag aan anderen over. ‘Ik heb de laatste tijd veel gedroomd over schaken. Ik ben klaar om verder te gaan met mijn leven’, zegt hij tegen The Harvard Gazette.
Donutbord
De algoritmes die Simkin ontwikkelde, kunnen ook op andere gebieden van pas komen. Zo nam de beroemde Nederlandse wiskundige Edsger Dijkstra het achtdamesprobleem in 1972 als voorbeeld om het nut van gestructureerd programmeren aan te tonen.
Naast het n-damesprobleem bestaan er meer varianten op het achtdamesprobleem. Je kunt het schaakbord bijvoorbeeld meer dan twee dimensies geven. Ook heeft de Hongaarse wiskundige György Pólya het probleem bestudeerd als je een schaakbord oprolt en de uiteinden aan elkaar vastmaakt, zodat het een donutvorm krijgt.
Simkin schaakt zelf ook, maar noemt zichzelf een verschrikkelijk slechte speler.
Het achtdamesprobleem
Hoe plaats je acht dames op een schaakbord zonder dat twee van die dames elkaar aanvallen? Dit achtdamesprobleem werd in 1848 opgeworpen door de Duitse schaker Max Bezzel in schaakkrant Schachzeitung.
Aangezien de dame in het schaken in alle richtingen kan bewegen, lijkt zo’n opstelling misschien lastig te realiseren. Toch zijn er maar liefst 92 verschillende manieren waarop dit kan. In 1850 plaatste wiskundige Franz Nauck in de Frankfurtse krant Illustrirte Zeitung als eerste alle oplossingen.
Sommige van die oplossingen verschillen niet echt van elkaar. Als je het schaakbord spiegelt of een aantal kwartslagen draait, gaan ze in elkaar over. Haal je die dubbelingen weg, dan blijven er twaalf unieke oplossingen over. Elf van die oplossingen hebben acht varianten. De twaalfde verandert niet als je het bord een halve slag draait en heeft daarom maar vier varianten.
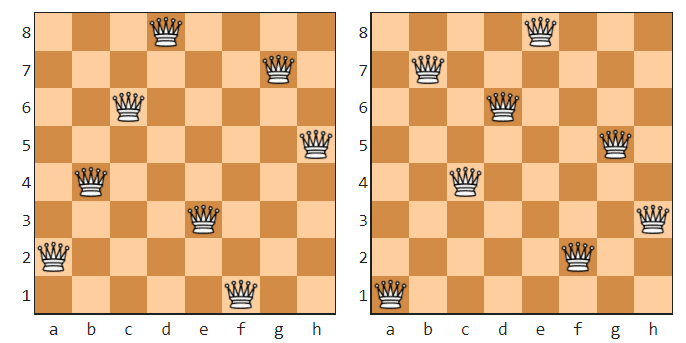
In 1874 bewees de Duitse wiskundige E. Pauls dat dit inderdaad alle oplossingen zijn. In 1850, kort na de introductie van het probleem, had zijn beroemde landgenoot Carl Friedrich Gauss al beschreven hoe zo’n bewijs eruit zou moeten zien. Gauss heeft het bewijs voor zover we weten echter nooit zelf voltooid, al beweerde hij in een brief aan een bevriende astronoom dat het ‘maar een uur of twee in beslag zou nemen’.
