Wij leven niet in één ruimtetijd, maar in drie. Met dat bizarre inzicht wil een Nederlandse natuurkundige ons begrip van de werkelijkheid volledig overhoop gooien.

Fysici weten het al meer dan honderd jaar zeker. Hoewel wij de wereld om ons heen in drie dimensies waarnemen, is het universum eigenlijk opgebouwd uit vier dimensies. We zien de drie ruimtelijke dimensies (links-rechts, op-neer en voor-achter), maar natuurkundigen kennen in hun formules een extra dimensie: de tijd (eerder-later). Samen vormen die vier dimensies de zogeheten ruimtetijd. Of het nu sterren of planeten zijn, huizen of mensen, onder alles schuilt die ruimtetijd. Zelfs in het ‘niets’, bijvoorbeeld de lege ruimte tussen sterren en sterrenstelsels, is de ruimtetijd aanwezig.
Die visie op de werkelijkheid begint echter te wankelen. Met een verse blik verwacht wiskundig-fysicus Walter van Suijlekom, verbonden aan de Radboud Universiteit in Nijmegen, de huidige ideeën over ruimtetijd op radicale wijze te doorbreken. Volgens hem is er namelijk niet slechts één ruimtetijd, maar zijn er wel drie. Aanwijzingen daarvoor borrelen volgens Van Suilekom op uit de wiskunde.

‘AI is een veredelde rekenmachine’
Met AI spoort Ann Dooms vervalste schilderijen op, maakt ze onleesbare teksten doorzoekbaar en brengt ze de kwaliteit van eicellen in kaart.
De gevolgen zijn immens. Als Van Suijlekom en zijn collega’s gelijk hebben,bestaat de wereld niet langer uit één stuk. In plaats daarvan werpt hij overal twee ‘schaduwen’, ofwel parallelle werelden die aan het blote oog worden onttrokken. Volgens dat idee leeft iedereen in drie parallelle werelden tegelijk, zonder dat we dat ooit doorhebben.
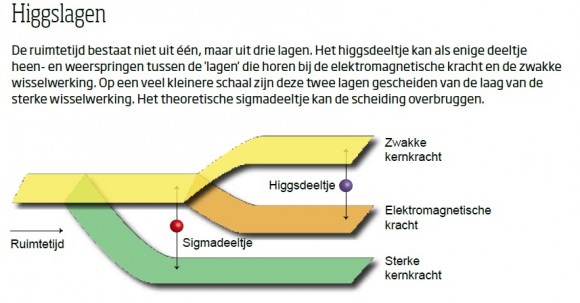
Wie verder inzoomt, ziet echter dat dat op sub-atomaire schaal heel anders is. Waar wij geen verschil zien tussen de drie lagen, bestaat dat verschil op deeltjesniveau wel. Daar zoeft het higgsdeeltje bijvoorbeeld zorgeloos van de ene laag naar de andere.
De beloften die Van Suijlekoms theorie met zich meebrengt, zijn groot. De theorie voorspelt bijvoorbeeld een ultrazwaar deeltje dat een fundamenteel probleem uit de natuurkunde kan oplossen. Belangrijker is nog dat het de algemene relativiteitstheorie en de deeltjesfysica in één wiskundige beschrijving weet te vatten. Mogelijk lukt het Van Suijlekom zelfs om zijn theorie toepasbaar te maken op de quantummechanica. Naar zo’n zogeheten quantumgravitatietheorie zijn fysici al meer dan een halve eeuw op zoek.
De oorsprong van de ideeën van Van Suijlekom en collega’s schuilt in een vakgebied met de naam niet-commutatieve meetkunde. Dat vakgebied zag in 1980 het levenslicht door het werk van de Franse wiskundige Alain Connes, winnaar van de Fields-medaille, de officieuze Nobelprijs voor de Wiskunde. Het cruciale verschil met de gewone meetkunde is dat de volgorde waarin wiskundige operaties worden uitgevoerd bepalend is voor de uitkomst. In de normale meetkunde maakt het niet uit of je 2 plus 3 uitrekent of 3 plus 2, maar in de niet-commutatieve meetkunde geeft een wisselende volgorde ook een andere uitkomst.
Die opmerkelijke eigenschap vormt de basis van Van Suijlekom’s alternatieve blik op de werkelijkheid. Een coördinaat stelt meestal iets concreets voor, bijvoorbeeld een locatie. Stel dat je op de rand staat van een vierkant zwembad, precies op een hoekpunt. Je kunt nu op twee manieren naar het hoekpunt aan de overkant lopen zonder nat te worden: door eerst naar voren te lopen en dan naar rechts of door eerst naar rechts te lopen en dan naar voren. Maar wanneer coördinaten niet langer commuteren, is de wereld minder logisch en kom je met ‘vooruit-dan-rechts’ ineens ergens anders uit dan met ‘rechts-dan-vooruit’.
Niet-commuterende dingen zijn in het dagelijks leven heel gewoon. Zo geeft ‘douchen en dan aankleden’ een volledig ander resultaat dan ‘aankleden, dan douchen’, terwijl de handelingen verder hetzelfde zijn.
Dat ‘niet-commuteren’ is volgens Van Suijlekom de sleutel tot het ontsluiten van zijn nieuwe theorie. Daarvoor werkt hij samen met grondlegger Connes en collega Ali Chamseddine. Ook heeft Van Suijlekom de handen ineengeslagen met een onderzoeksgroep van wiskundigen en fysici aan het IMAPP-instituut, het Nijmeegse instituut voor wiskunde, sterrenkunde en deeltjesfysica.
De niet-commutatieve meetkunde leidt in drie stappen tot het inzicht dat de ruimtetijd onmogelijk uit een enkele laag kan bestaan. De eerste stap is de aanname dat de coördinaten van de ruimtetijd niet langer commuteren. De reden om dat aan te nemen is dat dit het gemakkelijker maakt om binnen die ruimtetijd natuurkundige processen te beschrijven die ook niet commuteren.
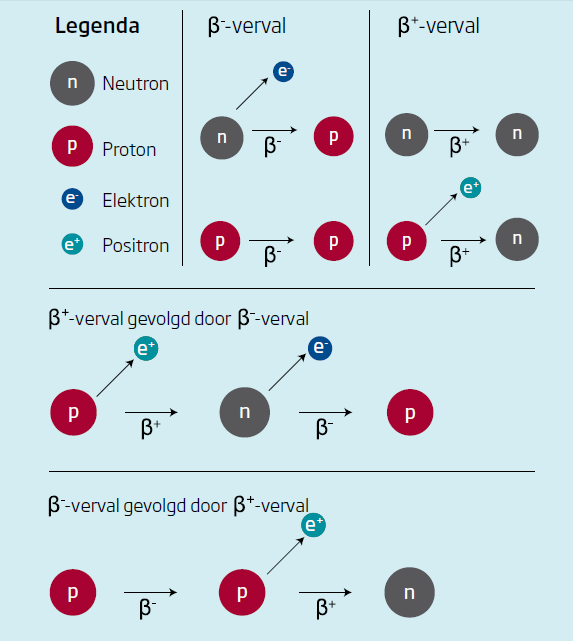
Een goed voorbeeld is bètaverval, een natuurkundige gebeurtenis waarbij een elementair deeltje een elektron of een positron uitstoot (zie grafiek in de afbeelding links). In de eerste variant stoot het deeltje een elektron uit – een proces dat bekend staat onder de naam bèta-min-verval. Als een neutron dat doet, wordt het een proton. Als echter een proton dat proces ondergaat, blijft het een proton, en gebeurt er dus verder niets. Bij het tweede geval, het uitstoten van een positron (bèta-plus-verval), vervalt een proton tot een neutron, en blijft een neutron een neutron. ‘Wanneer je beide processen na elkaar bekijkt, zie je dat bèta-plus na bèta-min ongelijk is aan bèta-min na bèta-plus’, zegt Van Suijlekom. Met andere woorden: bètaverval commuteert niet.
De tweede stap in de ontdekking van een gelaagde ruimtetijd is het besef dat bètaverval wordt veroorzaakt door de zwakke kernkracht, één van de vier fundamentele natuurkrachten. Wanneer je de ruimtetijd niet-commutatief maakt, zorgt dat ervoor dat die zich wiskundig hetzelfde gedraagt als de zwakke kernkracht. Daardoor kun je volgens Van Suijlekom stellen dat ‘een deeltje dat door niet-commutatieve ruimtetijd beweegt, als het ware een deeltje is dat is blootgesteld aan de effecten van de zwakke kernkracht.’
Higgsdeeltje
De derde en laatste stap is nu om die conclusie door te trekken. De zwakke kernkracht is namelijk niet de enige fundamentele natuurkracht. Twee andere fundamentele natuurkrachten, de elektromagnetische kracht en de sterke kernkracht, produceren ook niet-commuterende natuurkundige processen, zoals de zwakke kernkracht dat met bètaverval doet. Ook die processen kun je vangen in een beschrijving met niet-commuterende coördinaten binnen één laag van de ruimtetijd. ‘Op die manier vind je nog twee andere lagen’, zegt Van Suijlekom, zodat de ruimtetijd wel moet bestaan uit drie lagen.
Van Suijlekom kan zeer nauwkeurig de afstand tussen de drie lagen bepalen. ‘Het higgsdeeltje springt van de ene laag naar de andere’, zegt hij. Het doet dat tussen de lagen van de elektromagnetische kracht en de zwakke kernkracht. Van Suijlekom stelt dat de energie van het higgsdeeltje de afstand bepaalt die dat deeltje kan springen. Einsteins bekende formule E=mc2 stelt dat energie en massa moeiteloos in elkaar overgaan. Daarom drukt de deeltjesfysica massa’s van deeltjes ook uit in een hoeveelheid energie – in dit geval in aantallen GeV’s (giga-elektronvolts). Het higgsdeeltje heeft een massa van 125 GeV. Daaruit berekent Van Suijlekom dat het higgsdeeltje maximaal over 10-18 meter kan springen. Dat is volgens hem dan ook de afstand tussen de lagen van de elektromagnetische kracht en de zwakke kernkracht.
Hoe extreem klein die afstand is, blijkt zodra we die vergelijken met een atoomkern. Die is grofweg 10-10 meter groot – vele malen groter dus dan de afstand tussen die ruimtetijdlagen.
De afstand is zelfs zo klein dat die eigenlijk nog maar weinig betekenis heeft. ‘Waar meet je die afstand mee?’, vraagt Van Suijlekom zich hardop af. ‘Dat kan alleen met deeltjes, en die zijn groter dan de afstand waar het hier om gaat – behalve dan het higgsdeeltje.’
Bovendien suggereert het begrip afstand dat er iets tussen de lagen zit. Maar, benadrukt Van Suijlekom, dat is niet het geval. ‘Er zit geen ruimte tussen de lagen en er bestaat niet zoiets als een ruimte waarin deze lagen zich bevinden’, zegt hij. De lagen kunnen immers niet in een soort ruimtetijd liggen, want zij zijn zelf de ruimtetijd. De enige manier om van de ene laag naar de andere te komen, is tussen de lagen heen en weer springen zonder er ooit tussenin te belanden.
Maar hoe kom je dan in de derde laag? Het higgsdeeltje kan niet naar de laag van de sterke kernkracht springen. Het deeltje dat dat wel kan en zo de afstand tot die laag bepaalt, is het zogeheten sigmadeeltje.
Hoewel dat deeltje alleen nog op papier bestaat en vooralsnog in geen enkel experiment is gevonden, komt het niet zomaar uit de lucht vallen. Volgens Van Suijlekom is het een oplossing voor een bekend natuurkundig probleem. Nog voor het higgsdeeltje werd gevonden, volgde uit zijn theorie van de niet-commutatieve ruimtetijd dat het higgs een massa moest hebben van 168 GeV. Maar sinds vorig jaar is bekend dat het higgsdeeltje een massa van slechts 125 GeV heeft.
Deeltjesversneller
Dat het higgsdeeltje zo licht is, zorgt voor problemen. Het standaardmodel, het fysische model dat alle deeltjes en hun onderlinge interacties beschrijft, blijkt met een higgsdeeltje met die massa onzinnige uitkomsten te leveren wanneer fysici rekenen aan deeltjes met zeer hoge energie. ‘Maar met een extra deeltje kun je dat oplossen’, zegt Van Suijlekom. Dat sigmadeeltje volgt uit een wiskundige uitbreiding van het meetkundige model van Van Suijlekom en collega’s. Daaruit blijkt dat het sigmadeeltje extreem zwaar is: 1011 GeV. Daardoor is de afstand tussen de sterke kernkrachtslaag van de ruimtetijd en de andere twee heel klein: een ronduit onvoorstelbare 10-27 meter.
Dat het sigmadeeltje zo zwaar is, zorgt ervoor dat er geen deeltjesversneller bestaat die kan draaien met voldoende energie om dat deeltje waar te nemen. Van Suijlekom hoopt daarom dat het elders opduikt – bijvoorbeeld in het heelal, waar processen plaatsvinden met enorm veel energie. ‘We zouden het deeltje dan via een omweg kunnen vinden’, zegt hij.
Niet iedereen is ervan overtuigd dat het sigmadeeltje bestaat. ‘Van dat soort voorspellingen ben ik niet onder de indruk’, zegt theoretisch-fysicus Bert Schellekens, van het Nederlandse deeltjesfysica-instituut NIKHEF. Hoewel Schellekens benadrukt vertrouwen te hebben in de wetenschappelijke kwaliteiten van Connes, Chamseddine en Van Suijlekom, zet hij ook grote vraagtekens bij de voorspellingen van de niet-commutatieve ruimtetijd.
Schellekens: ‘Men heeft jarenlang gesproken over een higgsmassa van 168 GeV. Nu dat onjuist blijkt, wordt plotseling een extra deeltje uit de hoge hoed getoverd waarvan wordt beweerd dat het er altijd al is geweest en die de vorige voorspelling ongedaan maakt.’
Dat maakt hem ‘nogal sceptisch’ over nieuwe voorspellingen die uit dezelfde theorie voortkomen. Maar dat is het geval met alle alternatieve theorieën die op dit moment in omloop zijn. Schellekens: ‘Het standaardmodel werkt fantastisch, maar ik ken geen concrete voorspelling voor iets buiten dat standaardmodel die ik serieus neem.’
Ook theoretisch-fysicus Alexander Sevrin, verbonden aan de Vrije Universiteit Brussel benadrukt dat de niet-commutatieve ruimtetijd slechts één van de vele alternatieven is die de theoretische fysica te bieden heeft. ‘Er zijn heel veel ideeën over fysica voorbij het standaardmodel’, zegt Sevrin. ‘Dit is daar eentje van. Niettemin is het belangrijk dat een beperkt aantal wetenschappers deze aanpak verder uitspitten.’
Volgens Van Suijlekom is de belofte van zijn theorie voor de niet-commutatieve ruimtetijd in elk geval nog altijd groot. In 1996 publiceerde Connes samen met Chamseddine een artikel waarin de onderzoekers de niet-commutatieve meetkunde wisten toe te passen op de deeltjesfysica. In 2007 volgde een publicatie, samen met Matilde Marcolli van de Amerikaanse Caltech universiteit, waarin zij het volledige standaardmodel met de zwaartekracht wisten samen te voegen.
Dat resultaat had nog niemand behaald, maar in de wereld van de natuurkunde kreeg het nauwelijks aandacht. Volgens Van Suijlekom komt dat omdat de theorie zich nog altijd niet hield aan de wetten van de quantummechanica – en dat is hard nodig om een daadwerkelijk overkoepelende theorie te presenteren. ‘Daar wordt nu veel over nagedacht’, zegt Van Suijlekom.
Dat nadenken begint bij het werk van de beroemde Duitse fysicus Werner Heisenberg, die in 1927 aantoonde dat de snelheid en de locatie van een deeltje niet commuteren. Daarmee kende hij aan die deeltjes voor het eerst quantummechanisch gedrag toe, het zogeheten quantiseren, en legde Heisenberg de basis voor de moderne quantummechanica.
Helaas zijn velden in de fysica belangrijker dan deeltjes. De invloed van de elektromagnetische kracht is bijvoorbeeld te voelen in een veld en niet aan de hand van een deeltje. Het quantiseren van velden is echter heel moeilijk. Velden bestaan niet uit een eindig, maar uit een oneindig aantal punten, met elk een snelheid en locatie. ‘Het is vooralsnog onmogelijk om zelfs het elektromagnetische veld op een wiskundig nette manier te quantiseren’, zegt Van Suijlekom.
De wiskunde achter dat probleem is zelfs zo lastig dat het in een iets andere vorm werd opgenomen in de beruchte lijst van wiskundige millenniumproblemen. Die lijst bevat zeven extreem lastige wiskundeproblemen waarvoor het Amerikaanse Clay Mathematics Institute een beloning van een miljoen dollar per stuk beloofde aan de persoon die ze kan oplossen.
Van Suijlekom hoopt via de niet-commutatieve meetkunde ook meteen meer te weten te komen over de wiskunde achter het quantiseringsprobleem. Hij heeft zelfs al een aantal aanpakken bedacht die hij zo snel mogelijk wil uitproberen.
Limiet
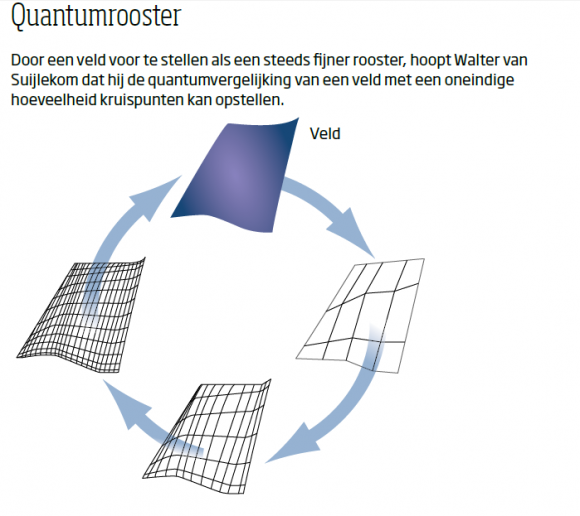
In een van die aanpakken doet hij alsof de ruimtetijd een rooster is met een eindige hoeveelheid punten, om het probleem wiskundig behapbaar te maken. Zijn idee is om de punten in dat rooster steeds dichter bij elkaar te brengen om zo op puur wiskundige wijze een quantumversie van zijn theorie op te stellen. ‘Ik wil daar dan de limiet van bestuderen, en zo de stap naar een continue oplossing zetten’, zegt Van Suijlekom.
Zo’n limiet is een beproefde mathematische tactiek om een uitkomst te krijgen die anders onhaalbaar zou zijn. Zo is de limiet van de rij breuken (1, 1/2, 1/4, 1/8, 1/16 enzovoort) gelijk aan nul. De waarde van de rij zakt langzaam naar nul, zonder die ooit te bereiken. Op dezelfde manier hoopt Van Suijlekom een veld met oneindig veel punten te quantiseren door te zoeken naar de limiet van een gequantiseerd veld met alsmaar meer punten.
Mocht dat niet werken, dan blijven volgens Van Suijlekom alternatieven over die vooralsnog niet voldoende zijn uitgewerkt om nu al met anderen te delen.
Daarnaast zoekt hij sinds kort nadrukkelijk de samenwerking met theoretisch-fysici die via andere wegen aan een overkoepelende theorie sleutelen. Dat loopt van snaartheoretici die hun heil zoeken in een oplossing met meerdere dimensies, tot quantumgravitatie-wetenschappers die de vreemde effecten van de quantummechanica op fundamenteel niveau in de ruimtetijd proberen in te bedden.
De Nijmeegse theoretisch-fysicus Wim Beenakker ziet bijvoorbeeld veel in de ideeën van Van Suijlekom. ‘Een ruimtetijd die uit drie lagen bestaat, zou een mooie verklaring zijn voor wat we in experimenten waarnemen’, zegt Beenakker. Samen met Van Suijlekom verkent hij het grensvlak tussen de wiskunde en natuurkunde.
Ook gaat Van Suijlekom samenwerken met de quantumgravitatiegroep in Nijmegen. ‘Zij hebben goede ideeën over hoe een quantummeetkunde eruit zou kunnen zien en wij hebben allerlei ideeën over een bredere wiskundige formulering. Allicht dat we elkaar kunnen helpen’, zegt hij.
Bovendien staat in oktober een workshop aan het Lorentz-instituut in Leiden op het programma, dat wiskundigen en fysici samenbrengt om over de natuurkundige gevolgen van zijn prille theorie te praten.
Of de theorie vervolgens ook beklijft, kan nog niemand zeggen, al lijken de radicale ideeën van Van Suijlekom en collega’s voorbestemd om de moderne fysica volledig op zijn kop te zetten.

