In de jaren zeventig berekenden natuurkundigen Stephen Hawking en Jacob Bekenstein wat de entropie, de mate van ‘wanorde’, van een zwart gat moet zijn. Nu hebben andere natuurkundigen eindelijk de quantumeffecten in kaart gebracht die verklaren waarom hun formule werkt.
Eindelijk begrijpen we hoe zwarte gaten aan hun entropie komen. Natuurkundigen bijten hun tanden hier al op stuk sinds het begin van de jaren zeventig, toen de beroemde wetenschapper Stephen Hawking en zijn collega Jacob Bekenstein berekenden hoeveel entropie, of ‘wanorde’, er in een zwart gat moet zitten. Met behulp van de quantummechanica hebben onderzoekers het probleem nu mogelijk opgelost.
‘Lange tijd dachten mensen dat je dit probleem alleen kon oplossen door allerlei fancy dingen in de snaartheorie te doen. Wij laten zien dat er een verzameling toestanden bestaat waarvoor dat niet nodig is’, zegt natuurkundige Vijay Balasubramanian van de Universiteit van Pennsylvania. ‘Het is buitengewoon eenvoudig, onverwacht zelfs.’
‘Als we iets buitenaards ontmoeten, dan is het een machine’
Oude sterren en pril leven – dat zijn de onderwerpen waar het hart van sterrenkundige Leen Decin harder van gaat kloppen.
Mate van wanorde
Entropie is een lastig begrip. Het zegt iets over het aantal ‘microtoestanden’ dat in een object voorkomt. Neem bijvoorbeeld een gaswolk. Om de entropie in het gas te berekenen, moet je weten hoeveel atomen de gaswolk bevat. Vervolgens bekijk je op hoeveel manieren die atomen gesorteerd kunnen zitten. Dat is, kort door de bocht, het aantal microtoestanden.
Op dezelfde manier proberen natuurkundigen uit te vogelen hoeveel entropie een zwart gat bevat door het aantal microtoestanden dat erin past te bepalen.
Balasubramanian en zijn collega’s maakten een model dat de microtoestanden in een zwart gat nabootst. Vervolgens vonden ze een formule om al deze toestanden te tellen, waardoor ze de totale entropie van het zwarte gat konden berekenen. Het aantal toestanden in een zwart gat met de massa van de zon is bijvoorbeeld ongeveer 27 × 1075 (waarbij 1075 een 1 is met 75 nullen erachter). Zij publiceerden hun vondst in het wetenschappelijke blad Physical Review Letters.
Tennisballen
Om je voor te stellen hoe de natuurkundigen de microtoestanden telden, kun je je elke toestand voorstellen als een tennisbal. ‘Als je in het zwarte gat kijkt, is daar veel ruimte, veel volume tussen de horizon en de singulariteit, dus je kunt je voorstellen dat je daar veel tennisballen in stopt’, zegt Balasubramanian. ‘Maar uiteindelijk stop je er veel te veel tennisballen in, en overschrijd je de entropie.’
Zwarte gaten zijn in werkelijkheid objecten die zich aan de regels van de quantummechanica houden. De tennisballenvergelijking gaat dus alleen op als ook de tennisballen zich ‘quantum’ gedragen. Quantumtennisballen zouden exotisch gedrag vertonen, waarbij ze minuscule tunnels in de ruimtetijd maken. Die zouden met elkaar verbonden raken via ‘quantumwormgaten’. Eenvoudiger gezegd betekent het dat de tennisballen met elkaar kunnen overlappen.
Door dit effect kunnen sommige quantumtoestanden worden voorgesteld als combinaties van andere toestanden. Daardoor zijn die toestanden niet meer noodzakelijk om de entropie van het zwarte gat te beschrijven. Ze kunnen dus geschrapt worden uit de telling. Toen de onderzoekers rekening hielden met deze quantumeffecten, vonden ze een aantal toestanden in de zwarte gaten dat overeenkwam met de Bekenstein-Hawking-formule.
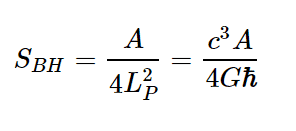
Hetzelfde basismechanisme zou moeten werken voor het tellen van het aantal microtoestanden van andere objecten, zegt zwarte-gaten-expert Don Marolf van de Universiteit van Californië in Santa Barbara. ‘Dit is een stevige stap in de goede richting; een belangrijke steen om op het pad te leggen.’
Paradoxen oplossen
Het tellen van het aantal toestanden in een zwart gat is niet alleen belangrijk om de entropie te berekenen. Het kan ook helpen om een kosmisch mysterie op te lossen dat de informatieparadox heet. Deze paradox stelt dat, omdat informatie niet verloren kan gaan, een zwart gat op de een of andere manier gegevens moet bewaren over wat erin is gevallen. Dat botst echter weer met andere natuurwetten.
‘Dit werk toont aan dat er een toestandsruimte bestaat die groot genoeg is om de informatie te bewaren’, zegt Balasubramanian. ‘De vraag die overblijft is: hoe komt die informatie weer vrij als het zwarte gat uiteindelijk verdampt?’
