Het was al bekend dat elektronen gek gedrag vertonen. Net als licht zijn ze soms golf, soms deeltje. Nu blijkt dat ze ook nog in dimensie 1,58 kunnen leven. Utrechtse natuurkundigen kregen de elektronen in deze niet-gehele dimensie gepropt door ze in de vorm van een fractal te rangschikken. Deze bijzondere elektronenstructuur kan toepassingen hebben in de elektronica.
Fractalen zijn wiskundige structuren waarvan het patroon zich blijft herhalen als je inzoomt. Deze vormen komen voor in de natuur. Bijvoorbeeld bij bomen waar de structuur van zijtakken aan een tak erg lijkt op die van takken die uit een boomstronk komen. Een van de bijzondere eigenschappen van fractalen is dat ze niet-gehele dimensies kunnen hebben. Daarover verderop meer.
Heino Falcke fotografeerde als eerste een zwart gat: ‘Nog mooier dan ik al die tijd had verwacht’
Heino Falcke, hoogleraar radioastronomie, maakte in 2019 de eerste foto van een zwart gat. Op dit moment doet hij onderzoek n ...
Repeterende driehoekjes
Wiskundigen (en kunstenaars zoals M.C. Escher) hebben zelf ook fractale structuren bedacht en ontworpen. Een daarvan is de Sierpińskidriehoek. Dit is de fractale structuur met dimensie 1,58 waarin de Utrechtse onderzoekers hun elektronen gerangschikt hebben.
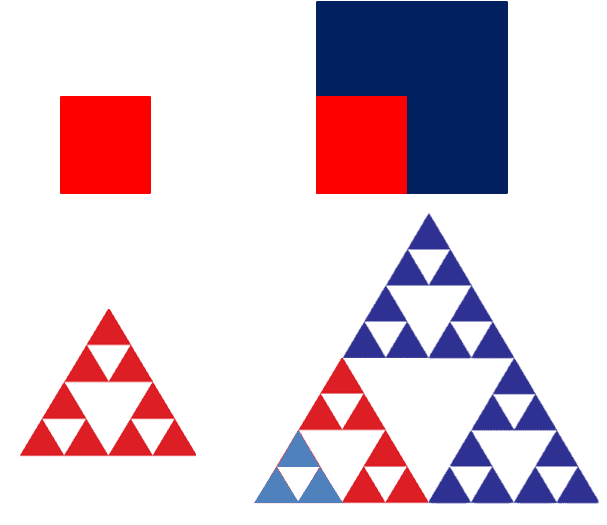
De Sierpińskidriehoek bestaat uit een basisdriehoekje waarvan het patroon zich in theorie tot in het oneindige kan blijven herhalen als je steeds verder uitzoomt. De basisvorm is een gelijkzijdige driehoek die opgebouwd is uit drie kleinere gelijkzijdige driehoekjes en in het midden een gat in de vorm van een omgekeerde driehoek.
Waarom heeft deze fractal nou dimensie 1,58? Hiervoor kijken we eerst naar de manier waarop dimensie twee bij vierkanten gedefinieerd kan worden. Als je de lengte en de breedte van een vierkant verdubbelt, dan heb je een groter vierkant met een oppervlak dat vier keer groter is. In dit nieuwe, grotere vierkant past het kleinere vierkantje precies vier keer. Wiskundigen zeggen dan dat je de dimensie log2(4)=2 is, oftewel 22=4 (verdubbeling tot de macht van de dimensie is het aantal kleine vierkantjes dat in de vergroting past).
De Sierpińskidriehoek kun je ook vergroten door de lengte en breedte te verdubbelen. Maar omdat het een fractal is, moet de vergroting er precies hetzelfde uitzien als het kleine Sierpińskidriehoekje. Dat betekent dat je in het midden een gat moet overlaten. Door dat gat passen er maar drie Sierpińskidriehoekjes in een grote Sierpińskidriehoek. De dimensie is dan log2(3)=1,58…, want 21,58…= 3.
Moleculen schuiven
Goed. We weten nu hoe wetenschappers zo’n gekke, niet-gehele dimensie definiëren. Maar hoe maak je zo’n ding met elektronen?
De onderzoekers knutselden de fractal in elkaar op een koperplaatje dat afgekoeld was tot -268°C. De elektronen op dat oppervlak kunnen vrij rondbewegen. Aan het plaatje voegden de onderzoekers koolstofmonoxidemoleculen toe. Die moleculen stoten elektronen af. ‘Het is als een omgekeerde muffin-bakvorm’, zegt Cristiane de Morais Smith, hoogleraar aan de Universiteit Utrecht. ‘De koolstofmonoxide zijn de uitstekende vormen en de elektronen schikken zich in de laaggelegen gebieden daaromheen.’
Met het elektrische veld van een scanning tunneling microscope (STM) kunnen de onderzoekers de koolstofmonoxidemoleculen oppakken en verplaatsen. Door de moleculen te rangschikken op de plekken waar de Sierpińskidriehoek gaten heeft, verzamelen de elektronen zich in de ruimtes daartussen en vormen zo een Sierpińskidriehoek.
Ter controle maten ze de elektronendichtheid aan het oppervlak. De elektronen blijken keurig in de Sierpińskidriehoek-vorm te blijven en dus, schrijven de onderzoekers, leven de deeltjes in dimensie 1,58.
Functionele fractalen
Wat hebben we aan een Sierpińskidriehoek van elektronen? Nog niet zoveel. ‘Het is nu nog fundamenteel onderzoek’, zegt De Morais Smith. ‘Maar ik denk dat er op de lang termijn toepassingen zullen zijn. Fractalen hebben hun nut al vaak bewezen.’ Er zijn bijvoorbeeld antennes met fractale vertakkingen. In verhouding met hun volume hebben fractalen namelijk een groot oppervlak. En omdat de structuur op kleine en grote schaal gelijk is, kunnen de antennes veel verschillende frequenties uitzenden en ontvangen.
Ten slotte is het bekend dat elektronen in één dimensie andere eigenschappen hebben dan in twee dimensies. Dit leidt tot verschillende elektronische toepassingen. De Morais Smith: ‘We willen nu gaan uitzoeken welke eigenschappen en mogelijke toepassingen elektronen in 1,58 dimensies hebben.’