Onderzoekers hebben een wiskundig model opgesteld van een deeltje dat nooit twee keer hetzelfde pad aflegt. Het model produceert verbluffend complexe patronen.
Nederlandse natuurkundigen hebben een wiskundige versie van biljart ontwikkeld waarin deeltjes nooit twee keer hetzelfde pad afleggen. De onvoorspelbare patronen waarin de deeltjes bewegen, kunnen ons helpen de complexe bewegingen van levende organismen beter te begrijpen.
Sommige dieren, waaronder mieren en slijmzwammen, laten bij het zoeken naar voedsel chemische sporen achter in hun omgeving. Dat voorkomt dat ze per ongeluk dezelfde route nog eens afleggen.
Dit is hoe we wiskundefobie te lijf kunnen gaan
Sarah Hart vertelt hoe we de angst voor getallen en formules weg kunnen nemen.
Natuurkundige Maziyar Jalaal van de Universiteit van Amsterdam en zijn collega’s hebben nu een wiskundig model gemaakt van dit gedrag. Ze ontdekten een onverwachte hoeveelheid complexiteit en chaos. Hun resultaten zijn gepubliceerd in het wetenschappelijk tijdschrift Physical Review Letters.
Wiskundig biljart
De natuurkundigen gebruikten als raamwerk een wiskundige vorm van biljart. Daarbij kaatst een oneindig klein deeltje heen en weer tussen de randen van een veelhoekige, wrijvingsloze ‘tafel’. De onderzoekers gaven het deeltje een ‘ruimtelijk geheugen’: als het een punt bereikte waar het al eerder was geweest, kaatste het onmiddellijk ervanaf, alsof het een muur tegenkwam.
De natuurkundigen leidden formules af die de beweging van zo’n deeltje beschrijven. Met deze formules maakten ze meer dan tweehonderd simulaties van de bewegingen. Zo zagen ze welk pad het deeltje aflegt in allerlei soorten veelhoeken, zoals een driehoek en een zeshoek. Hoewel het model eenvoudig, geïdealiseerd en deterministisch was, ontdekten de onderzoekers extreem ingewikkelde bewegingspatronen, zegt Jalaal.
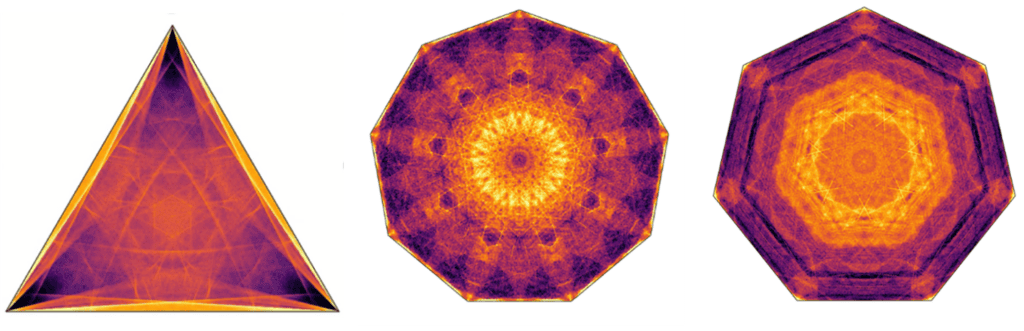
Binnen elke veelhoek ontdekten de natuurkundigen gebieden waarin de meeste deeltjes na lang rondstuiteren vast komen te zitten. Toen ze op die gebieden inzoomden, vonden ze nog meer bewegingspatronen. ‘Er komt geen einde aan de patronen die je ziet als je blijft inzoomen. En ze herhalen zich niet, het zijn geen fractals‘, zegt Jalaal.
Echte wereld
Wiskundige Katherine Newhall van de Amerikaanse Universiteit van North Carolina te Chapel Hill noemt het onderzoek een ‘interessant gedachte-experiment’. Het zou volgens haar alleen meer details moeten bevatten om organismen en objecten met een ruimtelijk geheugen in de echte wereld nauwkeurig weer te geven. Volgens Newhall zou een bestaand deeltje uiteindelijk in een niet helemaal rechte lijn bewegen, of wrijving ondervinden, waardoor de bewegingspatronen drastisch zouden veranderen of zelfs zouden verdwijnen.
