Twee Amerikaanse middelbare scholieren hebben de stelling van Pythagoras op vijf nieuwe manieren bewezen. Ze maakten hiervoor gebruik van regels uit de trigonometrie, ofwel driehoeksmeetkunde.
Toen Ne’Kiya Jackson and Calcea Johnson in hun laatste jaar van de middelbare school meededen aan een wiskundewedstrijd, hadden ze niet kunnen vermoeden dat dat zou leiden tot een publicatie in een wetenschappelijk vaktijdschrift. De bonusvraag van de wedstrijd luidde: ‘Ontwikkel een nieuw bewijs voor de stelling van Pythagoras.’ Met behulp van concepten uit de trigonometrie bedachten de studenten niet één, maar minstens vijf nieuwe bewijzen voor de stelling.
Cirkelredenering
Waarschijnlijk herinner je je de stelling van Pythagoras nog wel van de middelbare school. De stelling luidt a2 + b2 = c2 en biedt een handige manier om een zijde van een driehoek met een rechte hoek – een hoek van negentig graden – te berekenen wanneer de lengtes van de andere twee zijden bekend zijn. a en b zijn in dit geval de rechthoekszijden van zo’n driehoek en c de schuine zijde.

‘AI is een veredelde rekenmachine’
Met AI spoort Ann Dooms vervalste schilderijen op, maakt ze onleesbare teksten doorzoekbaar en brengt ze de kwaliteit van eicellen in kaart.
Er zijn verschillende manieren om de stelling van Pythagoras te bewijzen, maar tot nu toe lukte het slechts een handvol mensen om een bewijs te leveren op basis van trigonometrie. Bij trigonometrie gaat het om het begrijpen van en meten aan (drie)hoeken. Hierbij gebruiken wiskundigen de sinus en de cosinus van een hoek, die worden gedefinieerd als de verhouding van de overstaande en de schuine zijde, en de verhouding van de aanliggende en de schuine zijde respectievelijk.
Veel trigonometrische concepten en regels zijn gebaseerd op de stelling van Pythagoras. Het is daarom lastig om een trigonometrisch bewijs te vinden dat niet circulair is, oftewel een resultaat gebruikt om datzelfde resultaat te bewijzen.
Bovendien gebruiken wiskundeboeken vaak twee verschillende definities van de sinus- en cosinusfuncties door elkaar. De eerste definitie gaat uit van de hierboven beschreven concepten en definieert sinus en cosinus aan de hand van een driehoek met een rechte hoek en twee andere, scherpe hoeken die groter zijn dan nul. De tweede definitie maakt gebruik van de eenheidscirkel en is volgens Jackson en Johnson eerder ‘cyclotopisch’ dan trigonometrisch. Bewijzen gebaseerd op eigenschappen van de eenheidscirkel tellen dus eigenlijk niet als trigonometrisch bewijs. De leerlingen gingen daarom op zoek naar een bewijs van de stelling van Pythagoras dat alleen gebruikmaakt van die eerste definitie. Hun resultaten werden gepubliceerd in het wetenschappelijk tijdschrift The American Mathematical Monthly.
Driehoeken tekenen
Een van de eenvoudigere bewijzen voor de stelling van Pythagoras maakt gebruik van gelijkvormige driehoeken. Als je dezelfde strategie gebruikt om de stelling van Pythagoras met behulp van trigonometrie probeert te bewijzen, maak je het bewijs volgens Jackson en Johnson onnodig complex. Jan-Hendrik Evertse, wiskundige aan Universiteit Leiden, is het daarmee eens. ‘Je kunt zo’n bewijs vertalen naar sinus- en cosinusbegrippen, maar in feite worden die er dan met de haren bijgesleept.’
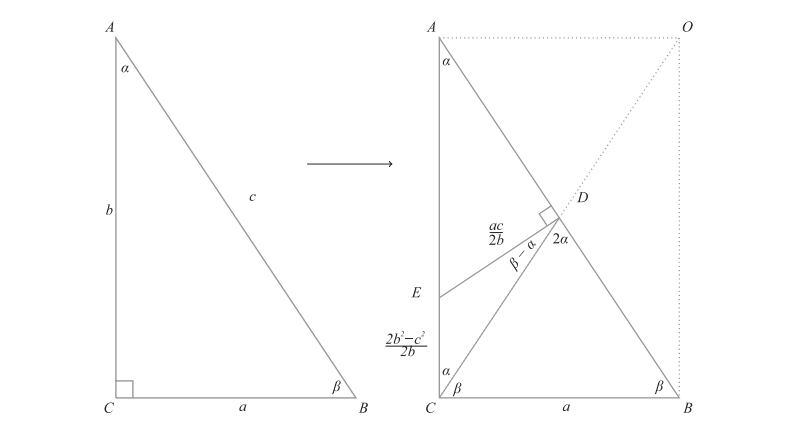
Jackson en Johnson gooiden het daarom over een andere boeg. Als uitgangspunt namen ze een hulpstelling waarvan ze aantoonden dat die altijd geldt. Deze stelt twee dingen. Ten eerste wordt duidelijk dat wanneer een driehoek gelijkbenig is en een rechte hoek heeft, de enig mogelijke driehoeken twee hoeken van 45 graden en een van 90 hebben. Ten tweede zegt de hulpstelling dat, als je bij een driehoek met een rechte hoek twee hoeken α en β kiest zodat α kleiner is dan β, er dan ook een rechthoekige driehoek bestaat met hoeken 2α en β – α.
De meeste van hun bewijzen zijn gebaseerd op het tweede deel van de hulpstelling, en gelden niet voor gelijkbenige rechthoekige driehoeken. Daarom bewezen Jackson en Johnson eerst dat de stelling van Pythagoras geldt voor alle gelijkbenige rechthoekige driehoeken. Met het tweede deel van het hulpstelling in hun achterhoofd, sloegen ze vervolgens aan het tekenen. Ze maakten allerlei driehoeksconstructies van driehoeken met hoeken 2α en β – α. Uit deze tekeningen leidden ze met behulp van calculus op vijf verschillende manieren af dat de stelling van Pythagoras altijd geldt bij een rechthoekige driehoek met scherpe hoeken. Ze zorgden er daarbij voor dat ze geen regels gebruikten die de stelling van Pythagoras veronderstellen.
Volgens Jackson en Johnson kun je via hun tekenmethode nog minstens vijf bewijzen voor de stelling vinden, maar die bewijzen ‘laten ze aan de geïnteresseerde lezer om te ontdekken’.
the Pythagorean Theorem, The American Mathematical Monthly, 131:9, 739-752, DOI:
10.1080/00029890.2024.2370240.
Toegankelijke wiskunde
Evertse: ‘Het is niet gebruikelijk dat middelbare scholieren een dergelijk artikel publiceren. Ik vond het een erg leuk artikel. Het brengt geen wiskundige doorbraken, maar het is goed geschreven en toegankelijk voor een breed publiek.
Wiskundige Klaas Pieter Hart van de Technische Universiteit Delft kan zich daarin vinden. ‘Het is moeilijk te zeggen hoe bijzonder het is wat ze hebben gedaan. Veel nieuwe bewijzen van de stelling van Pythagoras zijn terug te voeren op oudere bewijzen, maar met behulp van sinus en cosinus hebben de leerlingen als het ware een doorsteekje gevonden. Dankzij hun gebruik van sinus en cosinus worden bewijzen korter en overzichtelijker. Ze gebruiken sinus en cosinus als gereedschap, dat vind ik mooi.’
Inmiddels hebben beide scholieren de volgende stap gezet in hun carrière. Jackson studeert momenteel farmacie aan de Xavier-universiteit van Louisiana en Johnson is bezig met environmental engineering aan de staatsuniversiteit van Louisiana.

