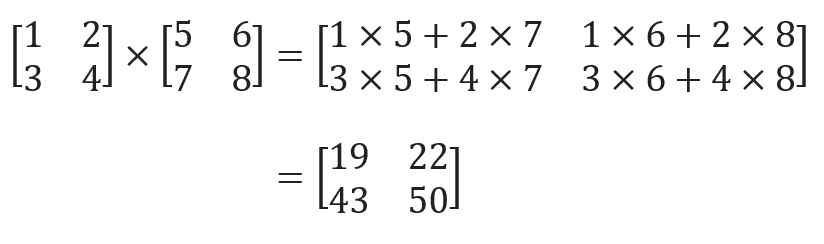Een kunstmatige intelligent systeem heeft een nieuwe methode gevonden voor matrixvermenigvuldiging, waarbij rijen en kolommen van getallen met elkaar worden vermenigvuldigd. Dit kan de rekensnelheid van computers met wel 20 procent verhogen.
Een kunstmatige intelligentie (AI) van het bedrijf DeepMind heeft een nieuwe manier ontdekt om getallenrasters (matrices) met elkaar te vermenigvuldigen. Het is voor het eerst in meer dan vijftig jaar dat er een doorbraak is op het gebied van deze ‘simpele’ wiskundige bewerking. Omdat dit type vermenigvuldiging de basis vormt van veel computertaken, kan de ontdekking de snelheid van sommige computerberekeningen met wel 20 procent verhogen.
Bij matrixvermenigvuldiging worden rijen en kolommen van getallen met elkaar vermenigvuldigd. Het is een rekentaak die in vrijwel alle software voorkomt – met name in grafische toepassingen, AI en wetenschappelijke simulaties. Zelfs een kleine verbetering van de efficiëntie van deze algoritmen zou flink wat energie kunnen besparen.
Heersen zwermen killerdrones straks over het slagveld?
Een luchtruim gevuld door kunstmatig intelligente killerdrones, die autonoom bepalen wie blijft leven en wie zal sterven. Hoe waarschijnlijk is dat?
Eerste doorbraak in vijftig jaar
Eeuwenlang werd aangenomen dat de meest efficiënte manier om matrices te vermenigvuldigen evenredig is met het aantal elementen dat moet worden vermenigvuldigd. Ofwel: hoe groter de matrices, hoe moeilijker de taak.
In 1969 bewees wiskundige Volker Strassen echter dat het vermenigvuldigen van twee matrices die elk uit twee rijen en twee kolommen bestaan niet noodzakelijkerwijs acht vermenigvuldigingen vergt. Met een slimme truc kan dat aantal worden teruggebracht tot zeven. Bij deze aanpak, die het strassenalgoritme heet, moet je weliswaar een extra optelling doen, maar dat is een klein offer: optellen kost een computer veel minder tijd dan vermenigvuldigingen.
Het strassenalgoritme is al meer dan vijftig jaar de meest efficiënte aanpak voor de meeste matrixgroottes. Er zijn wel enkele kleine verbeteringen gevonden, maar die zijn niet gemakkelijk in computercodes in te passen.
De AI van DeepMind, AlphaTensor geheten, heeft nu een snellere manier ontdekt die gewoon werkt op de huidige hardware. AlphaTensor kreeg de uitdaging om een werkend algoritme te bedenken dat de taak volbrengt in het kleinst mogelijke aantal stappen. De AI vond een algoritme om twee matrices van vier rijen en vier kolommen te vermenigvuldigen met slechts 47 vermenigvuldigingen. Dat is beter dan de 49 vermenigvuldigingen die nodig zijn in het algoritme van Strassen.
AlphaTensor ontwikkelde ook technieken voor matrices van andere groottes. In totaal wist hij voor zeventig verschillende matrixformaten nieuwe algoritmen te vinden.
Voor elke matrixgrootte ontdekte AlphaTensor duizenden werkende algoritmen. Voor de 4×4-matrices, bijvoorbeeld, vond hij er 14.000. Maar slechts een paar daarvan waren beter dan het huidige algoritme.
Intuïtieve AI
AI-wetenschapper Hussein Fawzi van DeepMind zegt dat de resultaten wiskundig kloppen, maar verre van intuïtief zijn voor mensen. ‘We weten eigenlijk niet waarom het systeem dit heeft bedacht’, zegt hij. ‘Waarom is dit de beste manier om matrices te vermenigvuldigen? Dat is onduidelijk.’
‘Op de een of andere manier ontwikkelt de AI een intuïtie voor wat er goed en slecht uitziet. Ik kan je eerlijk gezegd niet precies vertellen hoe dat werkt. Ik denk dat er nog wat theoretisch werk moet gebeuren voordat we begrijpen hoe AI dit soort dingen precies voor elkaar krijgt’, zegt Fawzi.
Energiewinst
De algoritmen kunnen de rekensnelheid van computeronderdelen met 10 tot 20 procent verhogen. Dat is onder meer getest met een grafische processor van computerproducent Nvidia en een tensorverwerkingseenheid van Google. Het is niet duidelijk of dergelijke winst ook te boeken is op gewone apparaten, zoals een smartphone of een laptop.
Computerwetenschapper James Knight van de universiteit van Sussex in het Verenigd Koninkrijk zegt dat allerlei soorten software die op supercomputers draaien, zoals AI-systemen en weersimulatie, in feite uit niets anders bestaan dan grootschalige matrixvermenigvuldiging. ‘Als deze aanpak daar wordt geïmplementeerd, zou dat de hele boel versnellen’, zegt hij.
Computerwetenschapper Oded Lachish van de universiteit van Londen onderstreept dat de nieuwe algoritmen de efficiëntie van veel software kunnen verbeteren, omdat matrixvermenigvuldiging zo’n veelvoorkomende bewerking is.
Meer AI-oplossingen
Bovendien zullen er waarschijnlijk meer nieuwe algoritmen volgen, zegt hij. ‘Ik denk dat we meer door AI bedachte oplossingen zullen zien voor andere problemen van vergelijkbare aard, ook al zal dat zelden iets zijn dat zo centraal staat als matrixvermenigvuldiging.’
‘Er is veel vraag naar zulke technologieën, want een minder zwaar algoritme betekent niet alleen snellere resultaten, maar ook minder energieverbruik’, zegt Lachish. Zo kun je een lichtere taak uitvoeren op kleinere, minder energieslurpende computers, ofwel op dezelfde computers, maar dan in minder tijd.
De prestatie van DeepMind betekent niet dat menselijke programmeurs zonder werk komen te zitten. ‘Moeten programmeurs zich zorgen maken? Misschien in de verre toekomst’, zegt Lachish. ‘Automatische optimalisatie wordt al tientallen jaren gedaan in de microchipindustrie. Dit is gewoon weer een belangrijk hulpmiddel voor de menselijke programmeur.’
MATRIXVERMENIGVULDIGING
Twee matrices vermenigvuldig je door steeds een rij van de eerste matrix te vermenigvuldigen met een kolom van de tweede matrix.
Neem bijvoorbeeld twee 2×2-matrices. Voor het eerste vakje (linksboven) van het resultaat vermenigvuldig je rij 1 van matrix 1 met kolom 1 van matrix 2. Je vermenigvuldigt daartoe het eerste getal van de eerste rij van matrix 1 met het eerste getal van de eerste kolom van matrix 2. Het resultaat tel je op bij de vermenigvuldiging van het tweede getal van de eerste rij van matrix 1 en het tweede getal van de eerste kolom van matrix 2. Voor het tweede vakje (rechtsboven) doe je hetzelfde, alleen neem je nu de getallen uit rij 1 van matrix 1 en kolom 2 van matrix 2. Zo kun je gaandeweg alle vier de vakjes vullen. 
