Een nieuw kunstmatig intelligent systeem kan op basis van meetgegevens zelfstandig natuurwetten formuleren. Op die manier herontdekte ‘AI-Descartes’ onder andere Keplers beschrijving van planeetbanen.
Een kunstmatig intelligent systeem heeft de derde wet van Kepler herontdekt. Deze wet toont het verband tussen de omlooptijd van twee hemellichamen en hun afstand tot elkaar. Het systeem, genaamd AI-Descartes, combineert data-analyse met bestaande theorieën. Naast Keplers wet vond het ook formules over klevende gasdeeltjes en bewegende klokken.
AI-assistent kan 113-hulpverlening ondersteunen
Dataspecialist Salim Salmi maakte een AI-tool die 113-hulpverleners ondersteunt.
Natuurkundigen streven ernaar alle natuurverschijnselen in wetten te vangen. Dat doen ze op twee manieren. Ten eerste proberen ze patronen te ontdekken in waarnemingen. Ten tweede leiden ze nieuwe formules af door bestaande wetten te combineren.
De belangrijkste natuurwetten, beschreven in onder andere de standaardmodellen van de deeltjesfysica en de kosmologie, zijn echter al tientallen jaren nauwelijks verbeterd. Dat komt onder andere doordat veel experimenten tegenwoordig een onoverzichtelijke brij aan data opleveren; denk aan de talloze deeltjesbotsingen in de Large Hadron Collider.
Uitschieters
Mogelijk kan kunstmatige intelligentie (AI) deze natuurkundige impasse helpen doorbreken. Er bestaan al diverse AI’s die patronen zoeken in grote hoeveelheden experimentele data.
Die gegevens zijn alleen vaak nogal rommelig. Ze bevatten rare uitschieters, die voortkomen uit meetfouten of eenmalige gebeurtenissen. Een planeet die rond een ster draait, kan bijvoorbeeld eventjes wiebelen doordat er een andere planeet bij in de buurt komt.
In hun zoektocht naar patronen nemen AI’s al die toevallige uitschieters mee. Daardoor leveren ze vaak extreem complexe formules aan, die weinig zeggen over de achterliggende natuurwetten. Ook vinden systemen vaak zoveel verschillende formules dat je er als onderzoeker tureluurs van wordt.
Wiskundige wetten
Met AI-Descartes hopen natuurkundigen deze problemen te omzeilen. Het systeem is ontwikkeld door een team onder leiding van Cristina Cornelio, onderzoeker bij Samsung AI in Cambridge (VK). De AI is vernoemd naar de zeventiende-eeuwse filosoof en wiskundige René Descartes, bekend van de spreuk ‘Ik denk, dus ik ben’. Hij had de destijds baanbrekende visie dat de natuur wordt geregeerd door wiskundige wetten die logisch uit elkaar volgen.
AI-Descartes leidt net als eerdere systemen formules af uit experimentele gegevens. Vervolgens kiest het systeem uit alle mogelijke formules het exemplaar dat het beste bij de bestaande theorieën past. ‘We combineren een benadering die al eeuwenlang door wetenschappers wordt gebruikt – nieuwe formules afleiden uit bestaande achtergrondtheorieën – met een datagestuurde benadering die gebruikelijker is in dit tijdperk van machine learning’, zegt Cornelio.
Exoplaneten en dubbelsterren
De onderzoekers gaven AI-Descartes NASA-gegevens van de beweging van de planeten in het zonnestelsel. Ook toonden ze het systeem hoe enkele planeten buiten het zonnestelsel rond hun ster bewegen, en hoe enkele dubbelsterren om elkaar heen draaien.
Op basis van die gegevens herontdekte AI-Descartes de derde wet van Kepler uit 1619 – en dan zelfs de verfijnde versie ervan, waarin de gravitatiewet van Newton uit 1687 wordt meegenomen. Keplers derde wet laat zien hoe twee hemellichamen, bijvoorbeeld een planeet en een ster, om elkaar heen draaien. De duur van een omloop hangt af van de afstand tussen de twee objecten en hun massa’s (zie het kader onderaan dit bericht).
De derde wet van Kepler is niet de ingewikkeldste formule in de natuurkunde – je kunt hem al op de middelbare school leren. Toch is het bijzonder dat een AI de wet uit waarnemingen heeft afgeleid. Bij de planeten in het zonnestelsel is het verband moeilijk te herkennen. Omdat ze veel minder zwaar zijn dan de zon, voldoen deze planeten namelijk aan een nog simpelere formule. Metingen van exoplaneten en dubbelsterren zijn dan weer minder nauwkeurig, zodat ze meer gekke uitschieters bevatten. Desondanks zetten de gegevens van dubbelsterren AI-Descartes op het juiste spoor.
Relativiteitstheorie
De onderzoekers hebben AI-Descartes ook losgelaten op twee complexere natuurkundige verschijnselen. Zo herontdekte het systeem een formule van de Amerikaanse scheikundige Irving Langmuir uit 1918. Die formule beschrijft hoe gasdeeltjes aan een vast oppervlak blijven kleven.
Verder mocht AI-Descartes op zoek naar een formule uit de speciale relativiteitstheorie van Albert Einstein (1905). De formule beschrijft hoe een bewegende klok een heel klein beetje langzamer loopt dan een stilstaande klok. Omdat dit effect nauwelijks meetbaar is, wist AI-Descartes niet de exacte formule op te stellen. Wel vond het systeem enkele formules die vrij dicht in de buurt komen. Ook concludeerde de AI op basis van de ingevoerde gegevens dat de lichtsnelheid constant moet zijn, een van de pijlers van Einsteins relativiteitstheorie.
Achteroverleunen
De huidige resultaten zijn vooral een bewijs dat een AI op basis van meetgegevens bruikbare natuurkundige wetten kan opstellen. Het ultieme doel is om AI-Descartes nieuwe wetten te laten ontdekken.
Daarvoor moet de AI eerst meer bestaande theorieën kennen. Omdat alle achtergrondkennis in de juiste computertermen aan het systeem moet worden gevoerd, kost dat nu nog veel tijd. Bovendien is een verkeerde invoer of een ontbrekend deel meteen fnuikend voor de resultaten.
De onderzoekers willen daarom AI-Descartes trainen om zelf wetenschappelijke artikelen te lezen en daaruit de bekende formules af te leiden. Als dat lukt, kunnen theoretisch natuurkundigen rustig achteroverleunen en zien of computers hun vakgebied verder op weg helpen. ‘Een van de spannendste aspecten van ons werk is de mogelijkheid om aanzienlijke vooruitgang te boeken in wetenschappelijk onderzoek’, zegt Cornelio.
Keplerkader
De derde wet van Kepler is in 1619 gepubliceerd door de Duitse astronoom Johannes Kepler. De wet laat zien hoe snel twee hemellichamen om elkaar heen draaien. Wanneer je hem combineert met de gravitatiewet van Newton (1687), is Keplers derde wet op verschillende manieren als formule te schrijven. Je kunt bijvoorbeeld uitgaan van de tijd waarin beide objecten een ronde volbrengen, zoals hieronder.
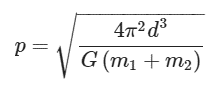
De omlooptijd (p) hangt af van de afstand tussen de twee hemellichamen (d) en de massa’s van beide objecten (m1 en m2). Verder bevat de formule de gravitatieconstante van Newton (G), een onveranderlijk getal dat aangeeft hoe sterk de zwaartekracht is.
Met deze formule kun je bijvoorbeeld uitrekenen hoe lang de aarde doet over een rondje om de zon. Je vult dan voor d de afstand in tussen de aarde en de zon (1,5 ∙ 1011 m) en voor m1 en m2 de massa’s van beide objecten (respectievelijk 6,0 ∙ 1024 kg en 2,0 ∙ 1030 kg). Daaruit rolt een waarde van ruim 31,5 miljoen seconden, oftewel ruim 365 dagen.
In dit geval kun je de massa van de aarde zelfs uit de formule weglaten, omdat die verwaarloosbaar is ten opzichte van de massa van de zon. Dat betekent dat de omlooptijd van een planeet in het zonnestelsel alleen afhangt van zijn afstand tot de zon. Ook als de aarde tien keer zo zwaar was geweest, had een jaar 365 dagen geduurd.
