In mijn eerste jaar Sterrenkunde kreeg ik het vak ‘Inleiding Astrofysica’ van Vincent Icke (tegenwoordig o.a. bekend van zijn gastoptredens in De Wereld Draait Door), die mij in één van zijn eerste colleges met één simpel gedachtenexperiment wist uit te leggen hoe hoog de hoogste berg kan worden en waarom grote, zware hemellichamen eigenlijk rond zijn.
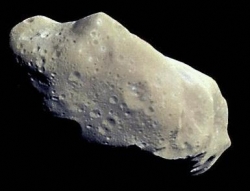
Met een melkpak de grootte van een astroïde schatten, kost maar enkele denkstappen
Dat experiment ging ongeveer als volgt: bedenk welk voorwerp nog net aan een touwtje kan hangen voordat het breekt. Is dat een koelkast? Een snoepje? Of meer iets in de orde van een pak melk? Bedenk vervolgens hoe zwaar dat voorwerp ongeveer is en hoe zwaar een stuk touw van – zeg – een meter ongeveer zal zijn. Vergelijk het in je hoofd met ongeveer even zware voorwerpen en je hebt al snel wat afgeschatte getalletjes gevonden. Daarnee kun je dab uitrekenen hoe lang het touw ongeveer zal zijn voordat het onder z’n eigen gewicht, door zijn eigen zwaartekracht, kapot wordt getrokken. Als je dezelfde schattingen gebruikt als wij destijds in college, kom je ongeveer op 10 kilometer uit. En verdomd: dat blijkt nog best aardig te kloppen ook! Dus als je een misvormde asteroïde ziet, denk dan aan het stukje touw en je weet hoe groot hij maximaal zal zijn.
Nieuwe vaccins tegen veroudering lijken ziekten als alzheimer te voorkomen
Onderzoekers werken aan vaccins die ziekten zoals kanker en alzheimer een halt moeten toeroepen. Wat mogen we hiervan verwachten?
Overigens blijkt dankzij ‘quantum decoherence’ het hele concept van Schödinger’s kat natuurlijk een beetje onzinnig, maar qua begrip van de basisprincipes van de quantummechanica is het gedachtenexperiment nog altijd wel effectief – sterker nog: het had hier best een voorbeeld kunnen zijn.
Een ander zeldzaam moment van inzicht volgde bij mijn keuzevak ‘quantum computing’, waarin ik voor een voordracht zelf eens ging uitzoeken waarom we eigenlijk niet allerhande gekke quantumeffecten zien in ons dagelijks leven. Waarom heeft mijn bankstel wél een gedefinieerde plaats (ook als ik er niet naar kijk – want geloof me, ik plof regelmatig ‘blind’ neer), maar een atoom niet? Het antwoord – met de mooie Engelse term quantum decoherence – was niet alleen inzichtelijk, maar sprak ook tot de verbeelding. Deeltjes kunnen – en zullen – verstrengeld raken met deeltjes in de omgeving en verliezen daardoor op de schaal waarop wij leven hun unieke quantumeigenschappen. En ta-da! Voortaan zou ik altijd min of meer snappen waarom wij niet in een quantumwereld leven (en waarom het onder andere zo moeilijk is om een quantum computer te bouwen).
Van Deense Dog tot Teckel: ineens is evolutie zo’n lastig concept niet meer
Nog zo’n voorbeeld is evolutie. Ik vond het op de middelbare school en tijdens grote gedeeltes van mijn studie altijd vréselijk moeilijk om me voor te stellen dat zo’n ééncellig organisme in een anonieme oersoep alle diversiteit op Aarde kan hebben voortgebracht (ik studeerde dan ook geen biologie). Maar toen las ik (het begin van) ‘On The Origin of Species’ over de ontwikkeling van de hondenrassen onder menselijke invloed (hetzelfde voorbeeld haalde Richard Dawkins overigens recentelijk aan in zijn nieuwe boek, ‘The Greatest Show on Earth’). En elke keer als ik nu denk aan evolutie, denk ik aan het enorme verschil tussen zo’n grote Deense Dog en een koddig kleine Teckel (of vergelijkbare andere rassen) die mensen er in luttele jaren handmatige selectie hebben weten uit te persen en de conclusie dat evolutie in een godsgruwelijk lange tijd alles van olifanten tot mieren heeft voortgebracht, is ineens minder vreemd.
Kortom: het bestaat, die effeciënte manier van uitleggen, dat briljante concept of die inzichtelijke vergelijking waarmee iets in één keer helder wordt. Ik heb weleens aan anderen gevraagd of zij zelf ook dergelijke momenten van inzicht kenden. Een soort ‘Eureka!-moment, lang nadat het oorspronkelijke idee wetenschappelijk voet aan wal kreeg. Meestal waren de antwoorden zelf weinig inzichtelijk – terwijl ik toch zeker weet dat anderen ze ook zullen hebben.
De powers of ten: veel duidelijker wordt de schaal van het Heelal niet.
Tot slot nog één voorbeeld dan: de grootte van ons universum. Nog altijd vind ik het vréselijk lastig om me voor te stellen hoe groot het heelal eigenlijk is, ondanks dat je als Sterrenkundige luchtig met ‘lichtjaren’, ‘roodverschuivingen’ en enorme gewichten, afstanden, maten en andere getallen strooit alsof het niks is. Maar pas vanaf de ‘powers of ten‘ lezing – niet voor niets een favoriet onder de publiekslezingen van Sterrenkundigen – kon ik me ook maar iets begínnen voor te stellen bij de absurde afmetingen waar ik als student dagelijks mee te maken had. Als ik in een zeldzaam romantische bui midden in de nacht (meestal na het uitgaan) nog eens omhoog staar en denk aan al die duizelingwekkende schalen – van planeet, naar zonnestelsel, naar sterrenstelsel, naar cluster, naar supercluster, enzovoorts – dan speelt altijd ergens op de achtergrond die beroemde fotosessie door mijn hoofd.
Mochten dit soort inzichten ooit een term nodig hebben, dan stel ik in de titel van dit blog alvast een (flauwe en onterecht enigzins negatief klinkende) naam voor. Wie weet een betere?