Een internationale groep wiskundigen heeft een nieuw model ontwikkeld: het ‘tropische zandhoopjesmodel’. Dit model biedt nieuwe hoop om aardbevingen te kunnen voorspellen en is hiertoe beter in staat dan het klassieke zandhoopjesmodel.
Stel je voor dat je in een kermisattractie zit waarbij een lange arm je rondjes laat draaien, net zolang tot je niet meer weet wat boven en onder is. Als je het geluk hebt naast een wiskundige te zitten, zal deze je, terwijl je met een duizelingwekkend tempo naar beneden valt, enthousiast proberen uit te leggen dat dit een systeem is met twee evenwichtspunten.
Het ene evenwicht bevindt zich op de plek waar je vlak boven de grond wordt ingesnoerd. Dit is een stabiel evenwicht; een windvlaag of een duw kan je een beetje heen en weer doen schommelen, maar veel meer gebeurt er niet. Heel anders is het op het moment dat de arm je heeft meegenomen naar het hoogste punt. Genietend van het mooie uitzicht weet je dat, als er geen rem op de attractie zou zitten, er maar een klein zuchtje wind nodig zou zijn om de arm uit balans te brengen en in vliegende vaart naar beneden te doen storten. Dit is een voorbeeld van een kritisch evenwicht.

Deeltjesfysicus Dylan van Arneman: ‘Ik ben op zoek naar iets wat misschien niet bestaat’
Dylan van Arneman verruilt een paar keer per jaar zijn werkkamer op het Science Park in de Watergraafsmeer voor de ondergrond ...

Zelforganiserende kritische systemen
In bovenstaande situatie is het duidelijk wie jou in die kritische situatie heeft gebracht; de eigenaar van de kermisattractie. Maar in de wereld komen ook een hele hoop fenomenen voor die zichzelf in een kritische toestand brengen. Neem bijvoorbeeld aardbevingen. Door opbouwende krachten op de breuklijnen van aardplaten kan soms uit het niets een kritische situatie ontstaan, waardoor er maar een klein zetje nodig is om een aardbeving te doen ontstaan en een groot gebied om te toveren tot een woest schuddend geheel. Het is bijna onmogelijk om te voorspellen wanneer dit precies zal gebeuren.
Wiskundigen gebruiken het ‘zandhoopjesmodel’ om dit soort systemen te beschrijven. Het gaat hier niet daadwerkelijk om een echt hoopje zand, maar – hou je vast – om een virtueel mathematisch hoopje zand, dat het gedrag van allerlei soorten dynamische systemen reproduceert.

Mathematische hoopjes zand
Hoe ziet dat er dan uit, zo’n model met mathematische hoopjes zand? Je kunt bijvoorbeeld een schaakbord nemen, met op elk hoekpunt van vakjes een aantal korrels. Hoe meer korrels je toevoegt op een hoekpunt, hoe groter het hoopje zand. Maar er komt een punt dat de bende in elkaar kukelt als je nog een korrel toevoegt, en het hoopje zich verspreidt over naburige hoekpunten. Wiskundigen houden van eenvoud (al zou je dat niet altijd zeggen), dus laten we aannemen dat elk hoekpunt maximaal drie zandkorrels kan bevatten. Als er een vierde korrel op valt, wordt er naar elk buurhoekpunt één korrel gestuurd. Het hoekpunt waar de korrel op viel is nu leeg. Als één van de buren al drie korrels bevatte, stort dat hoopje ook in, en zo kun je een lawine aan instortingen krijgen, totdat het evenwicht is hersteld.
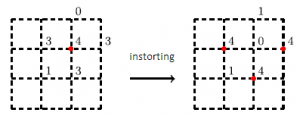
Met dit model kun je een bepaalde beginsituatie nemen, een zandkorrel op een willekeurige plek toevoegen, en kijken hoeveel instortingen er plaatsvinden totdat het evenwicht is bereikt. Hoe groter de lawine aan instortingen, des te kritischer de oorspronkelijke staat was: een kleine verandering als het toevoegen van één korrel heeft immers grote gevolgen. Afhankelijk van de beginsituatie ontstaan er allerlei interessante patronen.
Lawines en aardbevingen
Het zandhoopjesmodel voldoet aan dezelfde wetten als zelforganiserende kritische systemen zoals in het geval van aardbevingen. Hoe vaak een aardbeving van een bepaalde sterkte voorkomt, is vergelijkbaar met hoe vaak een lawine van een bepaalde grootte voorkomt op het schaakbord. Hierdoor zijn berekeningen aan het relatief simpele zandhoopjesmodel te vertalen naar veel ingewikkeldere systemen in de geofysica, kosmologie, economie en het risicomanagement. Wiskundigen gebruiken dit model al jaren om zelforganiserende kritische systemen te beschrijven. Het model is helaas niet in staat om concrete voorspellingen te doen voor bijvoorbeeld het plaatsvinden van aardbevingen. Daarom heeft een internationale groep wiskundigen nu een nieuw model voorgesteld, het ‘tropische zandhoopjesmodel’.

€ 19,99
Bestel in onze webshop
‘Er is een connectie gemaakt tussen twee wiskundige gebieden die tot nu toe nog niet verbonden waren’, zegt Frank Redig, hoogleraar toegepaste kansrekening aan de TU Delft. ‘De auteurs hebben deze connectie rigoureus gemaakt en dat is een enorm goede prestatie.’
Tropische hoopjes zand
Vertel je aan die wiskundige naast je in de kermisattractie dat je een tropische vakantiebestemming hebt, dan zal hij niet zo snel regenwouden voor zich zien, maar denken aan geometrische en algebraïsche objecten met specifieke eigenschappen. Het vakgebied van de tropische geometrie komt aan deze exotische naam simpelweg doordat grondlegger Imre Simon van Braziliaanse afkomst was.
Het nieuwe model gebruikt eigenlijk helemaal geen zandhoopjes meer, maar een ‘tropische curve’. Deze curve bestaat uit met elkaar verbonden rechte lijnstukjes, omsloten door een vierkant: een soort spinnenweb in een raamkozijn. De wiskundigen voegen punten toe in het vierkant en de figuur herorganiseert zichzelf zodanig dat er over elk punt een lijn heen valt. Hoe groter de aanpassing, hoe kritischer het systeem was.

Met dit nieuwe model is het eenvoudiger om voorspellingen te doen voor het gedrag van zelf-organiserende kritische systemen uit de echte wereld, zoals aardbevingen. Je hoeft alleen het gedrag van tektonische platen nog te vertalen naar het toevoegen van puntjes in een spinnenweb. Simpel toch? Voor de wiskundige op de kermis, die ondertussen verlekkerd naar de suikerspinnenkraam staat te kijken, in ieder geval wel.
